Introduction
The focal point of this short exposition will be an elaboration of the basic \(\ell_1\) penalization problem discussed in Willard (2017), \[\begin{equation} \operatorname*{argmin}_{\beta} \left\{ \frac{1}{2} \|y - X \beta\|^2_2 + \lambda \|\beta\|_1 \right\} \;. \label{eq:lasso} \end{equation}\] We continue our discussion on topics concerning automation and symbolic computation in Theano (Bergstra et al. 2010), as well as the mathematical methodology we believe is suitable for such implementations. Again, our framing of the problem is in terms of “proximal methods” (Parikh and Boyd 2014; Combettes and Pesquet 2011). Along the way we propose one simple means of placing the well-known technique of coordinate descent within the scope of proximal methods via a general property of proximal operators. These efforts are a continued outgrowth of our work in Polson, Scott, and Willard (2015).
Proximal and Computational Components
First, we [re]-introduce the workhorse of proximal methods: the proximal operator.
\[\begin{equation*} \operatorname*{prox}_{\phi}(x) = \operatorname*{argmin}_{z} \left\{ \frac{1}{2} \left(z - x\right)^2 + \phi(z) \right\} \;. \end{equation*}\]
Inspired by Equation \(\eqref{eq:lasso}\), we produce a toy dataset as follows:
from theano import shared as tt_shared
M = 50
M_nonzero = M * 2 // 10
beta_true = np.zeros(M)
beta_true[:M_nonzero] = np.exp(-np.arange(M_nonzero)) * 100
N = int(np.alen(beta_true) * 0.4)
X = np.random.randn(N, M)
mu_true = X.dot(beta_true)
y = mu_true + sc.stats.norm.rvs(np.zeros(N), scale=10)
X_tt = tt_shared(X, name='X', borrow=True)
y_tt = tt_shared(y, name='y', borrow=True)
# Estimation starting parameters...
beta_0 = np.zeros(X.shape[1]).astype('float64')
# Gradient [starting] step size
alpha_0 = 1. / np.linalg.norm(X, 2)**2
# np.linalg.matrix_rank(X)
# Regularization value heuristic
# beta_ols = np.linalg.lstsq(X, y)[0]
# lambda_max = 0.1 * np.linalg.norm(beta_ols, np.inf)
lambda_max = np.linalg.norm(X.T.dot(y), np.inf)As in Willard (2017), we can start with a model defined within a system like PyMC3 (Salvatier, Wiecki, and Fonnesbeck 2016).
with pm.Model() as lasso_model:
beta_rv = pm.Laplace('beta', mu=0, b=1,
shape=X.shape[1])
y_rv = pm.Normal('y', mu=X_tt.dot(beta_rv), sd=1,
shape=y.shape[0], observed=y_tt)In this setting one might then arrive at the necessary steps toward estimation automatically (i.e. identify the underlying \(\ell_1\) estimation problem). We discuss this more in Willard (2017).
For simplicity, we’ll just assume that all components of the estimation problem are know–i.e. loss and penalty functions. The proximal operator that arises in this standard example is the soft thresholding operator. In Theano, it can be implemented with the following:
def tt_soft_threshold(beta_, lambda_):
return tt.sgn(beta_) * tt.maximum(tt.abs_(beta_) - lambda_, 0)This operator can take other forms and the one used here is not particularly special. For instance, the maximum can be replaced by other conditional-like statements–such as \[\begin{equation*}
\operatorname{S}(z, \lambda) =
\begin{cases}
{\mathop{\mathrm{sgn}}}(\beta) (\beta - \lambda) & \beta > \lambda
\\
0 & \text{otherwise}
\end{cases}
\;.
\end{equation*}\] If we were to–say–multiply the output of this operator with another more difficult to compute result, then we might also wish to “optimize” this implementation by pushing the multiplication into the definition of the operator and altogether avoid its computation in the \(\beta \leq \lambda\) case.
Barring any reuses of this quantity, or a need to preserve undefined results produced by an expensive product with zero, we would really like a “compiler” to make such an optimization itself. It isn’t clear how a standard compiler–or interpreter/hybrid–could safely make this optimization, whereas it does seem more reasonable as a symbolic/Theano optimization.
Optimizations like this are–I think–a necessary step to enable expressive, generalized methods and truly rapid prototyping at the math level.
Now, assuming that we’ve obtained the relevant loss and penalty functions–for example, in PyMC3–then we can proceed by setting up the exact context of our proximal problem.
from theano import clone as tt_clone
# Clone the negative log-likelihood of our observation model.
nlogl_rv = -lasso_model.observed_RVs[0].logpt
nlogl = tt_clone(nlogl_rv)
nlogl.name = "-logl"
beta_tt = tt_inputs([nlogl])[4]Proximal Gradient
In what follows it will be convenient to generalize a bit and work in terms of arbitrary loss and penalty functions \(l\) and \(\phi\), respectively, which in our case corresponds to \[\begin{equation*} \begin{gathered} l(\beta) = \frac12 \|y - X \beta\|^2_2, \quad \text{and}\; \phi(\beta) = \|\beta\|_1 \;.\end{gathered} \end{equation*}\]
The proximal gradient (Combettes and Pesquet 2011) algorithm is a staple of the proximal framework that provides solutions to problems of the form \[\begin{equation*} \operatorname*{argmin}_\beta \left\{ l(\beta) + \lambda \phi(\beta) \right\} \;, \end{equation*}\] when both \(l\) and \(\phi\) are lower semi-continuous convex functions, and \(l\) is differentiable with Lipschitz gradient.
The solution is given as the following fixed-point: \[\begin{equation} \beta = \operatorname*{prox}_{\alpha \lambda \phi}(\beta - \alpha \nabla l(\beta)) \;. \label{eq:forward-backward} \end{equation}\] The constant step size \(\alpha\) is related to the Lipschitz constant of \(\nabla l\), but can also be a sequence obeying certain constraints. Since our \(l\) under consideration is \(\ell_2\), we have the incredibly standard \(\nabla l(\beta) = X^\top (X \beta - y)\).
Implementation
As in Willard (2017), we provide an implementation of a proximal gradient step.
from theano import function as tt_function
from theano.compile.nanguardmode import NanGuardMode
tt_func_mode = NanGuardMode(nan_is_error=True,
inf_is_error=False,
big_is_error=False)
def prox_gradient_step(loss, beta_tt, prox_func,
alpha_tt=None, lambda_tt=None,
return_loss_grad=False,
tt_func_kwargs={'mode': tt_func_mode}
):
r""" Creates a function that produces a proximal gradient step.
Arguments
=========
loss: TensorVariable
Continuously differentiable "loss" function in the objective
function.
beta_tt: TensorVariable
Variable argument of the loss function.
prox_fn: function
Function that computes the proximal operator for the "penalty"
function. Must take two parameters: the first a
TensorVariable
of the gradient step, the second a float or Scalar value.
alpha_tt: float, Scalar (optional)
Gradient step size.
lambda_tt: float, Scalar (optional)
Additional scalar value passed to `prox_fn`.
TODO: Not sure if this should be here; is redundant.
"""
loss_grad = tt.grad(loss, wrt=beta_tt)
loss_grad.name = "loss_grad"
if alpha_tt is None:
alpha_tt = tt.scalar(name='alpha')
alpha_tt.tag.test_value = 1
if lambda_tt is None:
lambda_tt = tt.scalar(name='lambda')
lambda_tt.tag.test_value = 1
beta_grad_step = beta_tt - alpha_tt * loss_grad
beta_grad_step.name = "beta_grad_step"
prox_grad_step = prox_func(beta_grad_step, lambda_tt * alpha_tt)
prox_grad_step.name = "prox_grad_step"
inputs = []
updates = None
if isinstance(beta_tt, tt.sharedvar.SharedVariable):
updates = [(beta_tt, prox_grad_step)]
else:
inputs += [beta_tt]
if not isinstance(alpha_tt, tt.sharedvar.SharedVariable):
inputs += [alpha_tt]
if not isinstance(lambda_tt, tt.sharedvar.SharedVariable):
inputs += [lambda_tt]
prox_grad_step_fn = tt_function(inputs,
prox_grad_step,
updates=updates,
**tt_func_kwargs)
res = (prox_grad_step_fn,)
if return_loss_grad:
res += (loss_grad,)
return resStep Sizes
A critical aspect of the proximal gradient approach–and most optimizations–involves the use of an appropriate step size, \(\alpha\). The step sizes needn’t always be fixed values and, because of this, we can search for a suitable value during estimation. Furthermore, in some cases, step sizes can be sequences amenable to acceleration techniques (Beck and Teboulle 2014).
Step sizes–and the values that drive them–have critical connections to the performance of an optimization method and do not simply ensure convergence. In that sense, the power of an implementation can depend on how much support it has for various types of step size sequences and when they can be/are used.
Often, acceptable ranges of step size values are derived from broad properties of the functions involved and their gradients (e.g. Lipschitz). When explicitly parameterized, these properties can give meaning to what some call “tuning parameters”. The connections between function-analytic properties and “tuning parameters” themselves highlight the need for more mathematical coverage/symbolic assessment within implementations. Currently, most tuning parameter act as stand-ins for information that’s theoretically obtained from the know functions.
In this spirit, one particularly relevant direction of work can be found in Theano’s experimental matrix “Hints”. Matrix-property hints like theano.sandbox.linalg.ops.{psd, spectral_radius_bound} are good examples of the machinery needed to automatically determine applicable and efficient \(\alpha\) constants and sequences.
For our example, we will simply use backtracking line-search.
def backtracking_search(beta_, alpha_,
prox_fn, loss_fn, loss_grad_fn,
lambda_=1, bt_rate=0.5, obj_tol=1e-5):
# alpha_start = alpha_
z = beta_
beta_start_ = beta_
loss_start_ = loss_fn(beta_)
loss_grad_start_ = loss_grad_fn(beta_)
while True:
beta_ = beta_start_ - alpha_ * loss_grad_start_
z = prox_fn(beta_, alpha_ * lambda_)
loss_z = loss_fn(z)
step_diff = z - beta_start_
loss_diff = loss_z - loss_start_
line_diff = alpha_ * (loss_diff -
loss_grad_start_.T.dot(step_diff))
line_diff -= step_diff.T.dot(step_diff) / 2.
if line_diff <= obj_tol:
return z, alpha_, loss_z
alpha_ *= bt_rate
assert alpha_ >= 0, 'invalid step size: {}'.format(alpha_)Routines–like this–that make use of the gradient and other quantities might also be good candidates for execution in Theano, if only for the graph optimizations that are able to remedy obviously redundant computations.
In this vein, we could consider performing the line-search, and/or the entire optimization loop, within a Theano scan operation. We could also create an Op that represents gradient and line-search steps. These might make graph construction much simpler and be more suited for the current optimization framework.
Although there’s no guarantee that scan and tighter Theano integrations will always produce better results than our current implementation, we wish to emphasize that it’s possible–given work in these symbolic directions.
Likewise, an Op for the proximal operator might also be necessary for solving many proximal operators found within a log-likelihood/objective function graph automatically and in closed-form. An effective implementation could be as simple as the use of lookup tables combined with some algebraic relationships/identities. State-of-the-art symbolic algebra libraries effectively use the same approach for symbolic integration.
Examples
First, to compute anything from our Theano graphs, we need to compile them to Theano functions.
lambda_tt = tt.scalar('lambda')
lambda_tt.tag.test_value = 1
prox_fn = tt_function([beta_tt, lambda_tt],
tt_soft_threshold(beta_tt, lambda_tt))
prox_grad_step_fn, loss_grad = prox_gradient_step(
nlogl, beta_tt, tt_soft_threshold,
return_loss_grad=True)
loss_fn = tt_function([beta_tt], nlogl)
loss_grad_fn = tt_function([beta_tt], loss_grad)
cols_fns = [
(lambda i, b: i, r'$i$'),
(lambda i, b: np.asscalar(loss_fn(b)),
r'$l(\beta^{(i)})$'),
(lambda i, b: np.linalg.norm(b - beta_true, 2),
r'$\|\beta^{(i)} - \beta^*\|^2_2$')
]For a baseline comparison–and sanity check–we’ll use the cvxpy library (Diamond and Boyd 2016).
import cvxpy as cvx
beta_var_cvx = cvx.Variable(M, name='beta')
lambda_cvx = 1e-2 * lambda_max * N
cvx_obj = cvx.Minimize(0.5 * cvx.sum_squares(y - X * beta_var_cvx)
+ lambda_cvx * cvx.norm(beta_var_cvx, 1) )
cvx_prob = cvx.Problem(cvx_obj)
_ = cvx_prob.solve(solver=cvx.CVXOPT, verbose=True)
beta_cvx = np.asarray(beta_var_cvx.value).squeeze()
loss_cvx = loss_fn(beta_cvx)
beta_cvx_err = np.linalg.norm(beta_cvx - beta_true, 2)We now have the necessary pieces to perform an example estimation. We’ll start with an exceedingly large step size and let backtracking line-search find a good value.
class ProxGradient(object):
def __init__(self, y, X, beta_0,
prox_fn_, loss_fn_, loss_grad_fn_,
alpha_0):
self.y = y
self.X = X
self.alpha_val = alpha_0
self.beta_0 = beta_0
self.N, self.M = X.shape
self.prox_fn_ = prox_fn_
self.loss_fn_ = loss_fn_
self.loss_grad_fn_ = loss_grad_fn_
def step(self, beta):
beta_val = np.copy(beta)
beta_val, self.alpha_val, _ = backtracking_search(
beta_val, self.alpha_val,
self.prox_fn_, self.loss_fn_, self.loss_grad_fn_)
return beta_valbeta_0 = np.zeros(M).astype('float64')
lambda_val = 1e-2 * lambda_max
pg_step = ProxGradient(y, X, beta_0,
lambda x, a: prox_fn(x, N * lambda_val * a),
loss_fn, loss_grad_fn, 10)
pg_cols_fns = cols_fns + [(lambda *args, **kwargs: pg_step.alpha_val,
r'$\alpha$')]
pg_est_data, _ = iterative_run(pg_step, loss_fn, pg_cols_fns)
pg_ls_data = pd.DataFrame(pg_est_data)
# pg_ls_data = pg_ls_data.append(pg_est_data, ignore_index=True)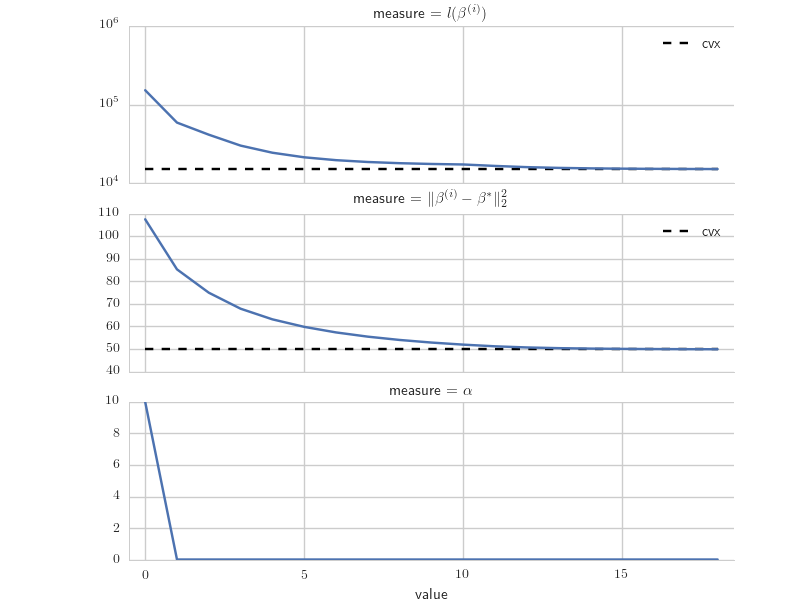
Figure \(\ref{fig:pg_ls_plot}\) shows a couple convergence measures for proximal gradient steps alongside the step size changes due to backtracking line-search. Regarding the latter, in our example a sufficient step size is found within the first few iterations, so the overall result isn’t too interesting. Fortunately, this sort of behaviour isn’t uncommon, which makes line-search quite effective in practice.
Coordinate-wise Estimation
Given that our loss is a composition of \(\ell_2\) and a linear operator of finite dimension (i.e. \(X\)), we can conveniently exploit conditional separability and obtain simple estimation steps in each coordinate. This is, effectively, what characterizes coordinate–or cyclic–descent. Since it is a common technique in the estimation of \(\ell_1\) models (Friedman et al. 2007; Mazumder, Hastie, and Tibshirani 2009; scikit-learn 2017), it’s worthwhile to consider how it can viewed in terms of proximal operators.
From a statistical perspective, the basics of coordinate-wise methods begin with the “partial residuals”, \(r_{-m} \in {{\mathbb{R}}}^{N}\) discussed in Friedman et al. (2007), and implicitly defined by \[\begin{equation} \begin{aligned} \beta^* &= \operatorname*{argmin}_{\beta} \left\{ \frac12 \| y - X(\beta - e_m \beta_m) - X e_m \cdot \beta_{m}\|^2_2 + \lambda \left|\beta_m\right| + \lambda \sum_{m^\prime \neq m} \left|\beta_{m^\prime}\right| \right\} \\ &= \operatorname*{argmin}_{\beta} \left\{ \frac12 \|r_{-m} - X e_m \cdot \beta_{m}\|^2_2 + \lambda \left|\beta_m\right| + \dots \right\} \;. \end{aligned} \label{eq:partial_resid} \end{equation}\] The last expression hints at the most basic idea behind the coordinate-wise approach: conditional minimization in each \(m\). Its exact solution in each coordinate is given by the aforementioned soft-thresholding function, which–as we’ve already stated–is a proximal operator. In symbols, \(\operatorname*{prox}_{\lambda \left|\cdot\right|}(x) = \operatorname{S}_\lambda(x)\), where the latter is the soft-thresholding operator.
Now, we can relate Equation \(\eqref{eq:partial_resid}\) to proximal methods through the proximal gradient fixed-point solution–i.e. Equation \(\eqref{eq:forward-backward}\)–and the following property of proximal operators:
\[\begin{equation*} \operatorname*{prox}_{\lambda \phi \circ e^\top_m}(z) = \sum^M_m \operatorname*{prox}_{\lambda \phi}\left(e^\top_m z\right) e_m \;. \end{equation*}\]
See Chaux et al. (2007).
The next result yields our desired connection.
For \(X\) such that \({{\bf 1}}^\top X e_m = 0\) and \(e^\top_m X^\top X e_m = 1\), \(m \in \{1, \dots, M\}\), the coordinate-wise step of the Lasso in Friedman et al. (2007 Equation (9)), \[\begin{equation*} \beta_m = \operatorname{S}_{\lambda}\left[ \sum_{n}^N X_{n,m} \left( y_n - \sum^M_{m^\prime \neq m} X_{n,m^\prime} \beta_{m^\prime} \right) \right] \;, \end{equation*}\] has a proximal gradient fixed-point solution under a Euclidean basis decomposition with the form \[\begin{equation*} \beta = \sum^M_m \operatorname*{prox}_{\alpha \lambda \phi}\left[ e^\top_m \left(\beta - \alpha \nabla l(\beta)\right) \right] e_m \;. \end{equation*}\]
We start with an expansion of the terms in \(\operatorname*{prox}_{\lambda \phi} \equiv \operatorname{S}_\lambda\). After simplifying the notation with \[\begin{equation*} \begin{gathered} \sum^N_{n} X_{n,m} z_n = e^\top_m X^\top z, \quad \text{and} \quad \sum^M_{m^\prime \neq m} X_{n,m^\prime} \beta_{m^\prime} = X \left(\beta - \beta_m e_m \right) \;, \end{gathered} \end{equation*}\] the expanded argument of \(\operatorname{S}\) reduces to \[\begin{equation*} \begin{aligned} e^\top_m X^\top \left(y - X\left( \beta - e_m \beta_m\right)\right) &= e^\top_m X^\top X e_m \beta_m + e^\top_m X^\top \left(y - X \beta\right) \\ &= \beta_m + e^\top_m X^\top \left(y - X \beta\right) \\ &= e^\top_m \left(\beta + X^\top \left(y - X \beta\right)\right) \end{aligned} \end{equation*}\] where the last step follows from \(X\) standardization. This establishes the relationship with Equation \(\eqref{eq:forward-backward}\) only component-wise. Using Lemma \(\eqref{lem:prox_ortho_basis}\) together with \(z = \beta - \alpha \nabla l(\beta)\) yields the proximal gradient fixed-point statement, i.e. \[\begin{equation*} \begin{aligned} \beta &= \sum^M_m \operatorname*{prox}_{\alpha \lambda \phi}\left[ e^\top_m \left(\beta - \alpha \nabla l(\beta)\right) \right] e_m \\ &= \sum^M_m \operatorname*{prox}_{\alpha \lambda \phi}\left( \beta_m + \alpha e_m^\top X^\top \left(y - X \beta \right) \right) e_m \;. \end{aligned} \end{equation*}\]
The property in Lemma \(\eqref{lem:prox_ortho_basis}\) can be used with other orthonormal bases–providing yet another connection between proximal methods and established dimensionality reduction and sparse estimation techniques (Chaux et al. 2007). Also, this property provides a neat way to think about \(X\)-based orthogonalizations in estimations for regression and grouped-penalization problems.
Implementation
The following performs a standard form of coordinate descent:
class CoordDescent(object):
def __init__(self, y, X, beta_0, prox_fn_, col_seq=None):
self.y = y
self.X = X
self.beta_0 = beta_0
self.N, self.M = X.shape
self.Xb = np.dot(self.X, self.beta_0)
self.prox_fn_ = prox_fn_
# (Inverse) 2-norm of each column/feature, i.e.
# np.reciprocal(np.diag(np.dot(X.T, X)))
self.alpha_vals = np.reciprocal((self.X**2).sum(axis=0))
if col_seq is None:
self.col_seq = np.arange(self.M)
def reset(self):
self.Xb = np.dot(self.X, self.beta_0)
def step(self, beta):
beta_val = np.copy(beta)
for j in self.col_seq:
X_j = self.X[:, j]
alpha_val = self.alpha_vals[j]
# A little cheaper to just subtract the column's
contribution...
self.Xb -= X_j * beta_val[j]
Xt_r = np.dot(X_j.T, self.y - self.Xb) * alpha_val
beta_val[j] = self.prox_fn_(np.atleast_1d(Xt_r),
alpha_val)
# ...and add the updated column back.
self.Xb += X_j * beta_val[j]
self.beta_last = beta_val
return beta_valOur example randomizes the order of coordinates to loosely demonstrate the range of efficiency possible in coordinate descent.
beta_0 = np.zeros(M).astype('float64')
lambda_val = 1e-2 * lambda_max
cd_step = CoordDescent(y, X, beta_0,
lambda x, a: prox_fn(x, N * lambda_val * a))
cd_cols_fns = cols_fns + [(lambda *args, **kwargs: j, "replication")]
pg_coord_data = pd.DataFrame()
for j in range(15):
est_data, _ = iterative_run(cd_step, loss_fn, cd_cols_fns)
pg_coord_data = pg_coord_data.append(est_data,
ignore_index=True)
# Reset internal state of our step method, since we're
# running multiple replications.
cd_step.reset()
np.random.shuffle(cd_step.col_seq)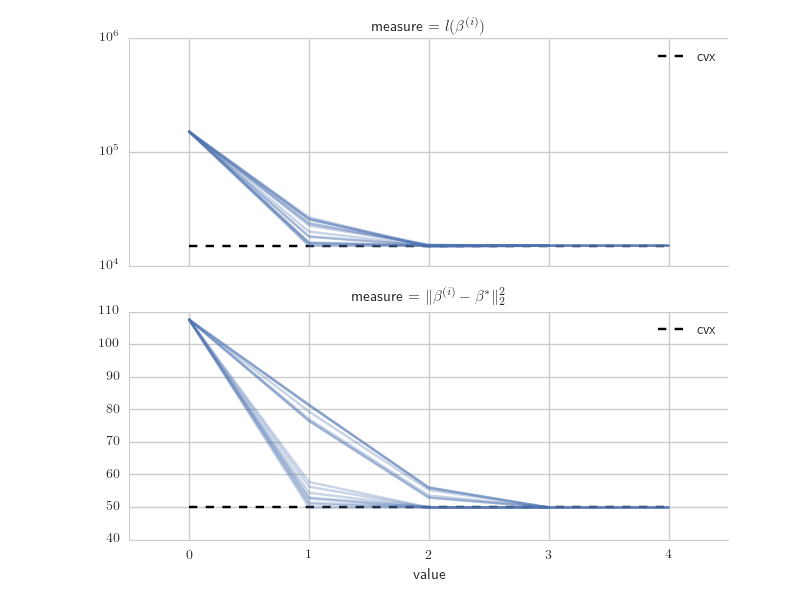
Figure \(\ref{fig:pg_coord_plot}\) shows convergence measures for each randomized coordinate order. The [average] difference in the number of iterations required for coordinate descent and proximal gradient is fairly noticeable. Nonetheless, both reach effectively the same limits.
Similar ideas behind batched vs. non-batched steps and block sampling–found within the Gibbs sampling literature (Roberts and Sahu 1997)–could explain the variation due to coordinate order and the relative efficiency of coordinate descent. There are also connections with our comments in Remark \(\ref{rem:bases}\) and, to some extent, stochastic gradient descent (SGD) (Bertsekas 2010).
In a woefully lacking over-generalization, let’s say that it comes down to the [spectral] properties of the composite operator(s) \(l \circ X\) and/or \(\nabla l \circ X\). These determine the bounds of efficiency for steps in certain directions and how blocking or partitioning the dimensions of \(\beta\) nears or distances from those bounds.
Regularization Paths
Also, due to the relatively fast convergence of coordinate descent, the method is a little more suitable for the computation of regularization paths– i.e. varying \(\lambda\) between iterations. There is much more to this topic, but for simplicity let’s just note that each \(\lambda\) step has a “warm-start” from the previous descent iteration–which helps–and that we’re otherwise fine with the solution provided by this approach.
Next, we make a small extension to demonstrate the computation of regularization paths–using lasso_path for comparison.
from sklearn.linear_model import lasso_path, enet_path
beta_0 = np.zeros(M).astype('float64')
lambda_path, beta_path, _ = lasso_path(X, y)
path_len = np.alen(lambda_path)
beta_last = beta_0
pg_path_data = pd.DataFrame()
for i, lambda_ in enumerate(lambda_path):
cd_path_step = CoordDescent(y, X, beta_last,
lambda x, a: prox_fn(x, N * lambda_ * a))
cd_cols_fns = cols_fns[1:] + [
(lambda *args, **kwargs: lambda_, r'$\lambda$')]
est_data, beta_last = iterative_run(cd_path_step, loss_fn,
cd_cols_fns,
stop_tol=1e-4,
stop_loss=True)
pg_path_data = pg_path_data.append(est_data.iloc[-1, :],
ignore_index=True)cd_cols_fns = cols_fns[1:] + [
(lambda *args, **kwargs: lambda_path[args[0]], r'$\lambda$')]
iter_values = []
for i, beta_ in enumerate(beta_path.T):
iter_values.append([col_fn(i, beta_)
for col_fn, _ in cd_cols_fns])
sklearn_path_data = pd.DataFrame(iter_values,
columns=zip(*cd_cols_fns)[1])
sklearn_path_data = sklearn_path_data.assign(
replication=None, type='sklearn')
pg_path_data = pg_path_data.assign(type='pg')
pg_path_data = pg_path_data.append(sklearn_path_data,
ignore_index=True)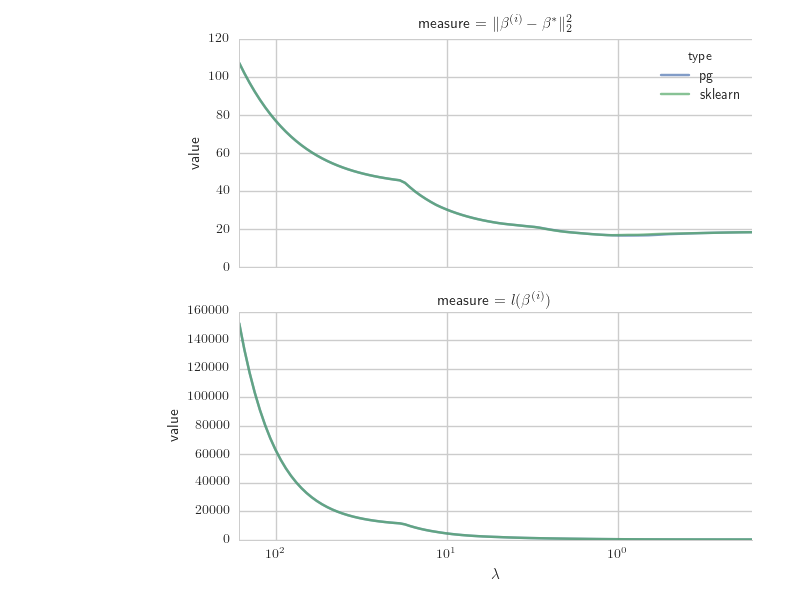
Discussion
Among the changes discussed earlier regarding Theano Ops for the proximal objects used here, we would also like to motivate much larger changes to the applied mathematician/statistician’s standard tools by demonstrating the relevance of less common–yet increasingly useful–abstractions. For instance, the proximal methods are neatly framed within operator theory and set-valued analysis, where concepts like the resolvent, sub-differential/gradient and others are common. Abstractions like these provide a compact means of extending familiar ideas into new contexts–such as non-differentiable functions.
Unfortunately, numerical libraries do not provide much in the way of utilizing these abstractions. Most are strictly founded in the representation of point-valued mappings, which can require significant work-arounds to handle even the most basic non-differentiable functions (e.g. the absolute value within our example problem). Our use of the proximal framework is, in part, motivated by its near seamless use and simultaneous bypassing of set-valued maps–in implementation, at least.
There is no fundamental restriction blocking support for set-valued maps, however–aside from the necessary labor and community interest. Even minimal support could provide a context that makes frameworks like ours merely minor abstractions. A similar idea can be found in the symbolic calculation of limits via filters (Beeson and Wiedijk 2005). Perhaps we can liken these changes to the modern evolution of linear algebra libraries to tensor libraries.
We would also like to stress that the value provided by the symbolic tools discussed here (Theano, really) are not just in their ability to act as compilers at a “math level”, but more for their ability to concretely encode mathematical characterizations of optimization problems and methods. Work in this direction is not new by any means; however, the combination of open-source tools and industry interest in algorithms that fall under the broad class of proximal methods (e.g. gradient descent, ADMM, EM, etc.) provides a more immediate reason to pursue these abstractions in code and automate their use.
Regarding the proximal methods, we can consider Theano optimizations that make direct use of the orthonormal basis property in Lemma \(\eqref{lem:prox_ortho_basis}\), or the Moreau-Fenchel theorem, and automate consideration for various estimation methods via splitting (e.g. ADMM, Douglas-Rachford, etc.)–perhaps by making decisions based on inferred or specified tensor, function, and operator properties. In future installments we’ll delve into the details of these ideas.
(Wytock et al. 2016) also discuss similar ideas in an optimization setting, such as the use of symbolic graphs and a close coupling with useful mathematical abstractions–including proximal operators. Additionally, there are many other good examples (Diamond and Boyd 2016) of constructive mathematical abstractions applied in code.
In most cases, libraries providing optimization tools and supporting model estimation do not attempt to root their implementations within an independently developed symbolic framework and then realize their relevant methodologies in that context. Too often the mathematical abstractions–or the resulting methods alone–are directly implemented at the highest levels of abstraction possible. This is what we see as the result of popular libraries like scikit-learn and the body of R packages. One can also find the same efforts for proximal methods themselves–e.g. in (svaiter 2017), where individual functions for ADMM, forward-backward/proximal gradient and Douglas-Rachford are the end result. This is the most common approach and it makes sense in terms of simplicity, but offers very little of the extensibility, generalization, or efficiencies provided by shared efforts across related projects and fields.
In the context of Theano, implementations immediately benefit from its code conversion, parallelization and relevant improvements to its basic graph optimizations. The latter covers both low-level computational efficiency–such as relevant application of BLAS functions–and high-level tensor algebra simplifications.
In a development community that builds on these tools, related efficiency and performance gains can occur much more often, without necessarily sacrificing the specificity inherent to certain areas of application. For example, we can safely use the Rao-Blackwell theorem as the basis of a graph optimization in PyMC3, so it could be included among that project’s default offerings; however, it would be far too cumbersome to use productively in a less specific context.
"References"
Beck, Amir, and Marc Teboulle. 2014. “A Fast Dual Proximal Gradient Algorithm for Convex Minimization and Applications.” Operations Research Letters 42 (1): 1–6. http://www.sciencedirect.com/science/article/pii/S0167637713001454.
Beeson, Michael, and Freek Wiedijk. 2005. “The Meaning of Infinity in Calculus and Computer Algebra Systems.” Journal of Symbolic Computation, Automated reasoning and computer algebra systems (ar-ca)AR-ca, 39 (5): 523–38. https://www.sciencedirect.com/science/article/pii/S074771710500026X.
Bergstra, James, Olivier Breuleux, Frédéric Bastien, Pascal Lamblin, Razvan Pascanu, Guillaume Desjardins, Joseph Turian, David Warde-Farley, and Yoshua Bengio. 2010. “Theano: A CPU and GPU Math Expression Compiler.” In Proceedings of the Python for Scientific Computing Conference (SciPy). Austin, TX.
Bertsekas, Dimitri P. 2010. “Incremental Gradient, Subgradient, and Proximal Methods for Convex Optimization: A Survey.” http://web.mit.edu/dimitrib/www/Incremental_Survey_LIDS.pdf.
Chaux, Caroline, Patrick L Combettes, Jean-Christophe Pesquet, and Valérie R Wajs. 2007. “A Variational Formulation for Frame-Based Inverse Problems.” Inverse Problems 23 (4): 1495.
Combettes, Patrick L, and Jean-Christophe Pesquet. 2011. “Proximal Splitting Methods in Signal Processing.” Fixed-Point Algorithms for Inverse Problems in Science and Engineering, 185–212.
Diamond, Steven, and Stephen Boyd. 2016. “CVXPY: A Python-Embedded Modeling Language for Convex Optimization.” Journal of Machine Learning Research 17 (83): 1–5.
Friedman, Jerome, Trevor Hastie, Holger Höfling, Robert Tibshirani, and others. 2007. “Pathwise Coordinate Optimization.” The Annals of Applied Statistics 1 (2): 302–32. http://projecteuclid.org/euclid.aoas/1196438020.
Mazumder, Rahul, Trevor Hastie, and Rob Tibshirani. 2009. “Regularization Methods for Learning Incomplete Matrices.” arXiv Preprint arXiv:0906.2034. https://arxiv.org/abs/0906.2034.
Parikh, Neal, and Stephen Boyd. 2014. “Proximal Algorithms.” Foundations and Trends in Optimization 1 (3): 123–231. https://doi.org/10.1561/2400000003.
Polson, Nicholas G., James G. Scott, and Brandon T. Willard. 2015. “Proximal Algorithms in Statistics and Machine Learning.” Statistical Science 30 (4): 559–81. http://projecteuclid.org/euclid.ss/1449670858.
Roberts, Gareth O., and Sujit K. Sahu. 1997. “Updating Schemes, Correlation Structure, Blocking and Parameterization for the Gibbs Sampler.” Journal of the Royal Statistical Society: Series B (Statistical Methodology) 59 (2): 291–317. http://onlinelibrary.wiley.com/doi/10.1111/1467-9868.00070/abstract.
Salvatier, John, Thomas V. Wiecki, and Christopher Fonnesbeck. 2016. “Probabilistic Programming in Python Using PyMC3.” PeerJ Computer Science 2 (April): e55. https://peerj.com/articles/cs-55.
scikit-learn. 2017. “Sklearn.Linear_model.ElasticNet Scikit-Learn 0.19.Dev0 Documentation.” http://scikit-learn.org/dev/modules/generated/sklearn.linear_model.ElasticNet.html\#sklearn-linear-model-elasticnet.
svaiter. 2017. “Pyprox.” https://github.com/svaiter/pyprox.
Willard, Brandon T. 2017. “A Role for Symbolic Computation in the General Estimation of Statistical Models.” https://brandonwillard.github.io/a-role-for-symbolic-computation-in-the-general-estimation-of-statistical-models.html.
Wytock, Matt, Steven Diamond, Felix Heide, and Stephen Boyd. 2016. “A New Architecture for Optimization Modeling Frameworks.” arXiv Preprint arXiv:1609.03488. https://arxiv.org/abs/1609.03488.
Comments
comments powered by Disqus