Introduction
Symbolic PyMC is a library that provides tools for symbolic manipulation of Tensor library models in TensorFlow (TF) and Theano. Over time, we plan to add tools that are mostly specialized toward Bayesian model manipulation and mathematical identities relevant to MCMC.
The main approach taken by symbolic-pymc is relational/logic programming powered by a miniKanren implementation in pure Python (based on the kanren package).
As an example of how symbolic-pymc’s offerings can be used, we’ll create a model “optimizer” that approximates the re-centering and re-scaling commonly demonstrated on a hierarchical normal model for the radon dataset. This optimization is symbolic and effectively produces another equivalent model with better sampling properties.
A similar example already exists in Theano and PyMC3; it can be found in the project README. In this case, we will operate on TF graphs via PyMC4 and approximate the same optimization using a very different approach targeted toward the log-likelihood graph.
To get started, we download the radon dataset and define the initial model in Listings 1, 2, and 3.
import numpy as np
import pandas as pd
import tensorflow as tf
import pymc4 as pm
import arviz as azdata = pd.read_csv('https://github.com/pymc-devs/pymc3/raw/master/pymc3/examples/data/radon.csv')
county_names = data.county.unique()
county_idx = data['county_code'].values.astype(np.int32)@pm.model
def hierarchical_model(data, county_idx):
# Hyperpriors
mu_a = yield pm.Normal('mu_alpha', mu=0., sigma=1)
sigma_a = yield pm.HalfCauchy('sigma_alpha', beta=1)
mu_b = yield pm.Normal('mu_beta', mu=0., sigma=1)
sigma_b = yield pm.HalfCauchy('sigma_beta', beta=1)
# Intercept for each county, distributed around group mean mu_a
a = yield pm.Normal('alpha', mu=mu_a, sigma=sigma_a, plate=len(data.county.unique()))
# Intercept for each county, distributed around group mean mu_a
b = yield pm.Normal('beta', mu=mu_b, sigma=sigma_b, plate=len(data.county.unique()))
# Model error
eps = yield pm.HalfCauchy('eps', beta=1)
# Expected value
#radon_est = a[county_idx] + b[county_idx] * data.floor.values
radon_est = tf.gather(a, county_idx) + tf.gather(
b, county_idx) * data.floor.values
# Data likelihood
y_like = yield pm.Normal('y_like', mu=radon_est, sigma=eps, observed=data.log_radon)
init_num_chains = 50
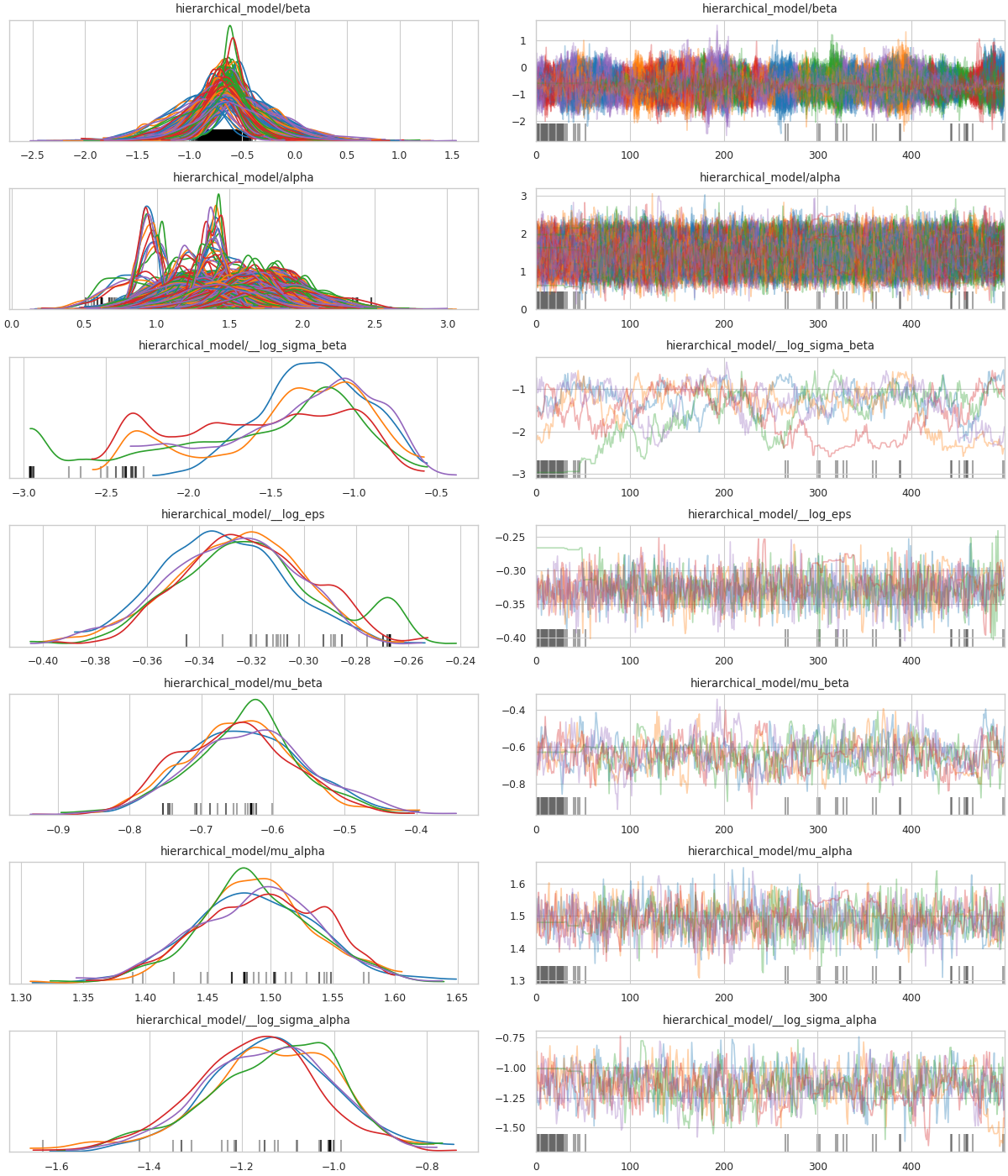
model = hierarchical_model(data, county_idx)In Listing 5, we estimate the model using the sample routine from PyMC4’s Radon example Notebook (reproduced in Listing 4). The same plots from the aforementioned notebook are also reproduced here in Figures 7 and 8.
def sample(model, init_num_chains=50, num_samples=500, burn_in=500):
init_num_chains = 50
pm4_trace, _ = pm.inference.sampling.sample(
model, num_chains=init_num_chains, num_samples=10, burn_in=10, step_size=1., xla=True)
for i in range(3):
step_size_ = []
for _, x in pm4_trace.items():
std = tf.math.reduce_std(x, axis=[0, 1])
step_size_.append(
std[tf.newaxis, ...] * tf.ones([init_num_chains] + std.shape, dtype=std.dtype))
pm4_trace, _ = pm.inference.sampling.sample(
model, num_chains=init_num_chains, num_samples=10 + 10*i, burn_in=10 + 10*i,
step_size=step_size_, xla=True)
num_chains = 5
step_size_ = []
for _, x in pm4_trace.items():
std = tf.math.reduce_std(x, axis=[0, 1])
step_size_.append(
std[tf.newaxis, ...] * tf.ones([num_chains]+std.shape, dtype=std.dtype))
pm4_trace, sample_stat = pm.inference.sampling.sample(
model, num_chains=num_chains, num_samples=num_samples, burn_in=burn_in,
step_size=step_size_, xla=True)
az_trace = pm.inference.utils.trace_to_arviz(pm4_trace, sample_stat)
return az_traceaz_trace = sample(model)import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib import rcParams
rcParams['figure.figsize'] = (11.7, 8.27)
# plt.rc('text', usetex=True)
sns.set_style("whitegrid")
sns.set_context("paper")_ = az.plot_energy(az_trace)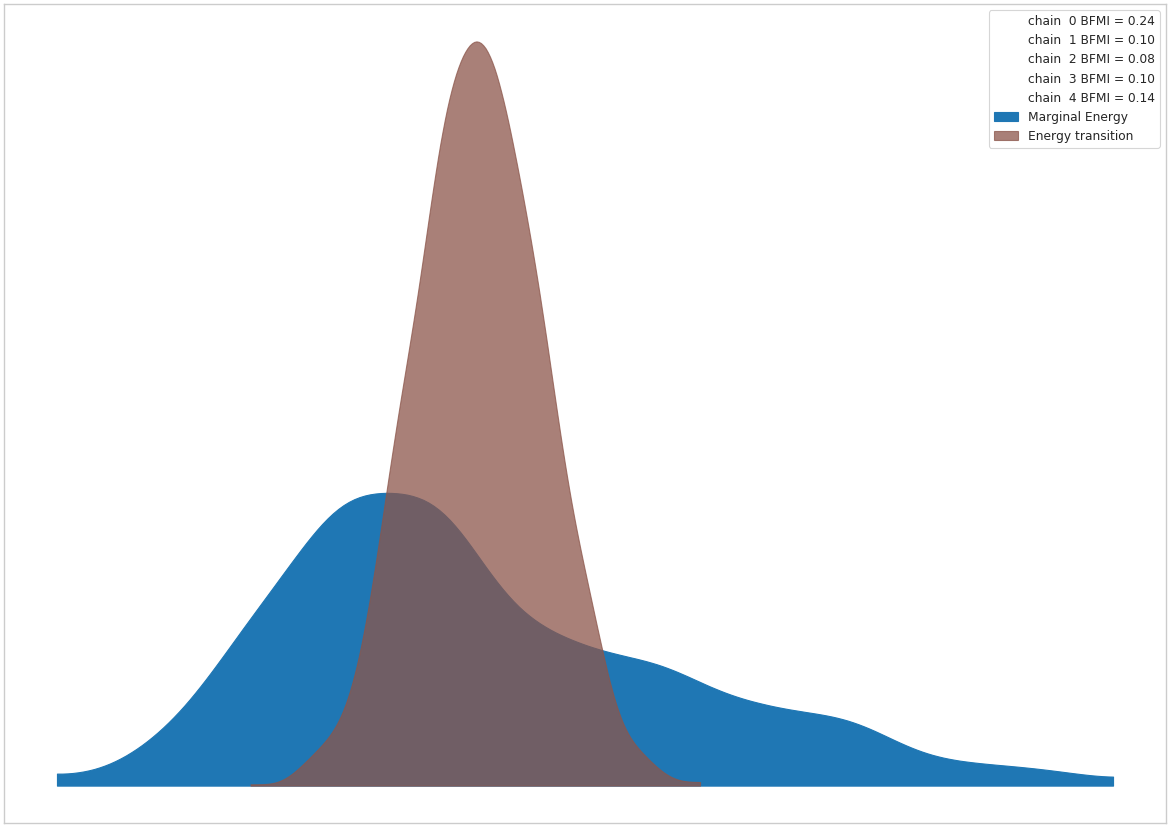
The Model’s Log-likelihood Graph
In order to apply our optimization, we need to obtain a graph of the log-likelihood function generated by the model in Listing 3. With the graph in-hand, we can perform the re-centering and re-scaling transform–in log-space–and produce a new log-likelihood graph that improves sampling.
This exercise introduces the TensorFlow function-graph backed by the class tensorflow.python.framework.func_graph.FuncGraph. FuncGraph is a subclass of the regular Graph objects upon which symbolic-pymc indirectly operates. Just like Theano’s FunctionGraphs, FuncGraph simply specializes a generic graph by specifying which constituent tensors are considered inputs and outputs.
In Listing 8, we use PyMC4’s internal mechanisms to build the log-likelihood function for our model and a corresponding list of initial values for the parameters.
state = None
observed = None
logpfn, init = pm.inference.sampling.build_logp_function(model,
state=state,
observed=observed)From here we need FuncGraphs for each input to logpfn. Since logpfn is a tensorflow.python.eager.def_function.Function instance, every time it’s called with a specific tensor it may create a new function-object with its own FuncGraph. In other words, it dynamically generates function objects based on the inputs it’s given.
This specialization process can be performed manually using logpfn.get_concrete_function(*args), which necessarily produces a tensorflow.python.eager.function.ConcreteFunction with the desired FuncGraph. Listing 9 creates and extracts these two objects.
logpfn_cf = logpfn.get_concrete_function(*init.values())
logpfn_fg = logpfn_cf.graphThe outputs are now available in graph form as logpfn_fg.outputs.
The Log-space Transform
Consider the following two equivalent hierarchical models,
\[\begin{equation} \begin{gathered} Y = X + \epsilon, \quad \epsilon \sim \operatorname{N}\left(0, \sigma^2\right) \\ X \sim \operatorname{N}\left(\mu, \tau^2\right) \end{gathered} \label{eq:model-1} \end{equation}\]
\[\begin{equation} \begin{gathered} Y = \mu + \tau \cdot \tilde{X} + \epsilon, \quad \epsilon \sim \operatorname{N}\left(0, \sigma^2\right) \\ \tilde{X} \sim \operatorname{N}\left(0, 1\right) \;. \end{gathered} \label{eq:model-2} \end{equation}\]
Models \(\eqref{eq:model-1}\) and \(\eqref{eq:model-2}\) are represented in (log) measure space, respectively, as follows:
\[\begin{align} \log p(Y, X) &= \log P(Y\mid X) + \log P(X) \nonumber \\ &= C - \frac{1}{2} \left(\frac{y}{\sigma} - \frac{x}{\sigma}\right)^2 - \frac{1}{2} \left(\frac{x}{\tau} - \frac{\mu}{\tau}\right)^2 \label{eq:log-model-1} \\ &= \tilde{C} - \frac{1}{2} \left(\frac{y}{\sigma} - \frac{\mu - \tau \cdot \tilde{x}}{\sigma}\right)^2 - \frac{1}{2} \tilde{x}^2 \label{eq:log-model-2} \;. \end{align}\]
Via term rewriting, Equation \(\eqref{eq:log-model-2}\) is produced–in part–by applying the replacement rule \(x \to \mu + \tau \cdot \tilde{x}\) to Equation \(\eqref{eq:log-model-1}\), i.e.
\[\begin{align*} \tilde{C} - \frac{1}{2} \left(\frac{y}{\sigma} - \frac{\mu + \tau \cdot \tilde{x}}{\sigma}\right)^2 - \frac{1}{2} \left(\frac{\mu + \tau \cdot \tilde{x}}{\tau} - \frac{\mu}{\tau}\right)^2 \;. \end{align*}\]
For consistency, the transform must also be applied to the \(dx\) term where/when-ever it is considered.
After a few algebraic simplifications, one obtains the exact form of Equation \(\eqref{eq:log-model-2}\).
Creating the miniKanren Goals
symbolic-pymc is designed to use miniKanren as a means of specifying mathematical relations. The degree to which an implementation of a mathematical relation upholds its known characteristics is–of course–always up to the developer. For the needs of PPLs like PyMC4, we can’t reasonably expect–or provide–capabilities at the level of automatic theorem proving or every relevant state-of-the-art symbolic math routine.
Even so, we do expect that some capabilities from within those more advanced areas of symbolic computing will eventually be required–or necessary–and we want to build on a foundation that allows them to be integrated and/or simply expressed. We believe that miniKanren is a great foundation for such work due to the core concepts it shares with symbolic computation, as well as its immense flexibility. It also maintains an elegant simplicity and is amenable to developer intervention at nearly all levels–often without the need for low- or DSL-level rewrites.
User-level development in miniKanren occurs within its DSL, which is a succinct relational/logic programming paradigm that–in our case–is entirely written in Python. This DSL provides primitive goals that can be composed and eventually evaluated by the run function. We refer the reader to any one of the many great introductions to miniKanren available at http://minikanren.org, or, for the specific Python package used here: this simple introduction.
For the matter at hand, we need to create goals that implement the substitution described above. The first step is to understand the exact TF graphs involved, and the best way to do that is to construct the relevant graph objects, observe them directly, and build “patterns” that match their general forms. Patterns are built with symbolic-pymc meta objects obtained from the mt helper “namespace”. Wherever we want to leave room for variation/ambiguity, we use a “logic variable” instead of an explicit TF (meta) object. Logic variables are created with var() and can optionally be given a string “name” argument that identifies them globally as a singleton-like object.
Inspecting the TF Graphs
In our case, the log-density returned by PyMC4–via the TensorFlow Probability library (TFP)– uses tf.math.squared_difference to construct the “squared error” term in the exponential of a normal distribution. This term contains everything we need to construct the substitution as a pair of TF graph objects.
Listing 10 shows the graph produced by a normal distribution in TFP.
import tensorflow_probability as tfp
from tensorflow.python.eager.context import graph_mode
from tensorflow.python.framework.ops import disable_tensor_equality
from symbolic_pymc.tensorflow.printing import tf_dprint
disable_tensor_equality()
with graph_mode(), tf.Graph().as_default() as test_graph:
mu_tf = tf.compat.v1.placeholder(tf.float32, name='mu',
shape=tf.TensorShape([None]))
tau_tf = tf.compat.v1.placeholder(tf.float32, name='tau',
shape=tf.TensorShape([None]))
normal_tfp = tfp.distributions.normal.Normal(mu_tf, tau_tf)
value_tf = tf.compat.v1.placeholder(tf.float32, name='value',
shape=tf.TensorShape([None]))
normal_log_lik = normal_tfp.log_prob(value_tf)tf_dprint(normal_log_lik)Tensor(Sub):0, shape=[None] "Normal_1/log_prob/sub:0"
| Tensor(Mul):0, shape=[None] "Normal_1/log_prob/mul:0"
| | Tensor(Const):0, shape=[] "Normal_1/log_prob/mul/x:0"
| | | -0.5
| | Tensor(SquaredDifference):0, shape=[None] "Normal_1/log_prob/SquaredDifference:0"
| | | Tensor(RealDiv):0, shape=[None] "Normal_1/log_prob/truediv:0"
| | | | Tensor(Placeholder):0, shape=[None] "value:0"
| | | | Tensor(Placeholder):0, shape=[None] "tau:0"
| | | Tensor(RealDiv):0, shape=[None] "Normal_1/log_prob/truediv_1:0"
| | | | Tensor(Placeholder):0, shape=[None] "mu:0"
| | | | Tensor(Placeholder):0, shape=[None] "tau:0"
| Tensor(AddV2):0, shape=[None] "Normal_1/log_prob/add:0"
| | Tensor(Const):0, shape=[] "Normal_1/log_prob/add/x:0"
| | | 0.9189385
| | Tensor(Log):0, shape=[None] "Normal_1/log_prob/Log:0"
| | | Tensor(Placeholder):0, shape=[None] "tau:0"
Instead of looking for the entire log-likelihood graph for a distribution, we can focus on only the SquaredDifference operators, since they contain all the relevant terms for our transformation.
More specifically, if we can identify “chains” of such terms, i.e. SquaredDifference(y, x) and SquaredDifference(x, mu), then we might be able to assume that the corresponding subgraph was formed from such a hierarchical normal model.
Listing 13 shows the SquaredDifference sub-graphs in the log-likelihood graph for our radon model. It demonstrates two instances of said SquaredDifference “chains”: they involve tensors named values_5 and values_1.
square_diff_outs = [o.outputs[0] for o in logpfn_fg.get_operations()
if o.type == 'SquaredDifference' or o.type.startswith('Gather')]
for t in square_diff_outs:
tf_dprint(t)Tensor(GatherV2):0, shape=[919] "GatherV2:0"
| Tensor(Placeholder):0, shape=[85] "values_3:0"
| Tensor(Const):0, shape=[919] "GatherV2/indices:0"
| | [ 0 0 0 ... 83 84 84]
| Tensor(Const):0, shape=[] "GatherV2/axis:0"
| | 0
Tensor(GatherV2):0, shape=[919] "GatherV2_1:0"
| Tensor(Placeholder):0, shape=[85] "values_2:0"
| Tensor(Const):0, shape=[919] "GatherV2_1/indices:0"
| | [ 0 0 0 ... 83 84 84]
| Tensor(Const):0, shape=[] "GatherV2_1/axis:0"
| | 0
Tensor(SquaredDifference):0, shape=[] "Normal_5/log_prob/SquaredDifference:0"
| Tensor(RealDiv):0, shape=[] "Normal_5/log_prob/truediv:0"
| | Tensor(Placeholder):0, shape=[] "values_1:0"
| | Tensor(Const):0, shape=[] "Normal/scale:0"
| | | 1.
| Tensor(RealDiv):0, shape=[] "Normal_5/log_prob/truediv_1:0"
| | Tensor(Const):0, shape=[] "Normal/loc:0"
| | | 0.
| | Tensor(Const):0, shape=[] "Normal/scale:0"
| | | 1.
Tensor(SquaredDifference):0, shape=[] "Normal_1_1/log_prob/SquaredDifference:0"
| Tensor(RealDiv):0, shape=[] "Normal_1_1/log_prob/truediv:0"
| | Tensor(Placeholder):0, shape=[] "values_4:0"
| | Tensor(Const):0, shape=[] "Normal_1/scale:0"
| | | 1.
| Tensor(RealDiv):0, shape=[] "Normal_1_1/log_prob/truediv_1:0"
| | Tensor(Const):0, shape=[] "Normal_1/loc:0"
| | | 0.
| | Tensor(Const):0, shape=[] "Normal_1/scale:0"
| | | 1.
Tensor(SquaredDifference):0, shape=[85] "SampleNormal_2_1/log_prob/Normal_2/log_prob/SquaredDifference:0"
| Tensor(RealDiv):0, shape=[85] "SampleNormal_2_1/log_prob/Normal_2/log_prob/truediv:0"
| | Tensor(Transpose):0, shape=[85] "SampleNormal_2_1/log_prob/transpose:0"
| | | Tensor(Reshape):0, shape=[85] "SampleNormal_2_1/log_prob/Reshape:0"
| | | | Tensor(Placeholder):0, shape=[85] "values_3:0"
| | | | Tensor(Const):0, shape=[1] "SampleNormal_2_1/log_prob/Reshape/shape:0"
| | | | | [85]
| | | Tensor(Const):0, shape=[1] "SampleNormal_2_1/log_prob/transpose/perm:0"
| | | | [0]
| | Tensor(Exp):0, shape=[] "exp_1/forward/Exp:0"
| | | Tensor(Placeholder):0, shape=[] "values_0:0"
| Tensor(RealDiv):0, shape=[] "SampleNormal_2_1/log_prob/Normal_2/log_prob/truediv_1:0"
| | Tensor(Placeholder):0, shape=[] "values_1:0"
| | Tensor(Exp):0, shape=[] "exp_1/forward/Exp:0"
| | | ...
Tensor(SquaredDifference):0, shape=[85] "SampleNormal_3_1/log_prob/Normal_3/log_prob/SquaredDifference:0"
| Tensor(RealDiv):0, shape=[85] "SampleNormal_3_1/log_prob/Normal_3/log_prob/truediv:0"
| | Tensor(Transpose):0, shape=[85] "SampleNormal_3_1/log_prob/transpose:0"
| | | Tensor(Reshape):0, shape=[85] "SampleNormal_3_1/log_prob/Reshape:0"
| | | | Tensor(Placeholder):0, shape=[85] "values_2:0"
| | | | Tensor(Const):0, shape=[1] "SampleNormal_3_1/log_prob/Reshape/shape:0"
| | | | | [85]
| | | Tensor(Const):0, shape=[1] "SampleNormal_3_1/log_prob/transpose/perm:0"
| | | | [0]
| | Tensor(Exp):0, shape=[] "exp_2_1/forward/Exp:0"
| | | Tensor(Placeholder):0, shape=[] "values_5:0"
| Tensor(RealDiv):0, shape=[] "SampleNormal_3_1/log_prob/Normal_3/log_prob/truediv_1:0"
| | Tensor(Placeholder):0, shape=[] "values_4:0"
| | Tensor(Exp):0, shape=[] "exp_2_1/forward/Exp:0"
| | | ...
Tensor(SquaredDifference):0, shape=[919] "Normal_4_1/log_prob/SquaredDifference:0"
| Tensor(RealDiv):0, shape=[919] "Normal_4_1/log_prob/truediv:0"
| | Tensor(Const):0, shape=[919] "Normal_4_1/log_prob/value:0"
| | | [0.8329091 0.8329091 1.0986123 ... 1.6292405 1.3350011 1.0986123]
| | Tensor(Exp):0, shape=[] "exp_3_1/forward/Exp:0"
| | | Tensor(Placeholder):0, shape=[] "values_6:0"
| Tensor(RealDiv):0, shape=[919] "Normal_4_1/log_prob/truediv_1:0"
| | Tensor(AddV2):0, shape=[919] "add:0"
| | | Tensor(GatherV2):0, shape=[919] "GatherV2:0"
| | | | Tensor(Placeholder):0, shape=[85] "values_3:0"
| | | | Tensor(Const):0, shape=[919] "GatherV2/indices:0"
| | | | | [ 0 0 0 ... 83 84 84]
| | | | Tensor(Const):0, shape=[] "GatherV2/axis:0"
| | | | | 0
| | | Tensor(Mul):0, shape=[919] "mul:0"
| | | | Tensor(GatherV2):0, shape=[919] "GatherV2_1:0"
| | | | | Tensor(Placeholder):0, shape=[85] "values_2:0"
| | | | | Tensor(Const):0, shape=[919] "GatherV2_1/indices:0"
| | | | | | [ 0 0 0 ... 83 84 84]
| | | | | Tensor(Const):0, shape=[] "GatherV2_1/axis:0"
| | | | | | 0
| | | | Tensor(Const):0, shape=[919] "mul/y:0"
| | | | | [1. 0. 0. ... 0. 0. 0.]
| | Tensor(Exp):0, shape=[] "exp_3_1/forward/Exp:0"
| | | ...
The names in the TFP graph are not based on the PyMC4 model objects, so, to make the graph output slightly more interpretable, Listing 15 attempts to re-association the labels.
from pprint import pprint
tfp_names_to_pymc = {i.name: k for i, k in zip(logpfn_cf.structured_input_signature[0], init.keys())}
pprint(tfp_names_to_pymc){'values_0': 'hierarchical_model/__log_sigma_alpha',
'values_1': 'hierarchical_model/mu_alpha',
'values_2': 'hierarchical_model/beta',
'values_3': 'hierarchical_model/alpha',
'values_4': 'hierarchical_model/mu_beta',
'values_5': 'hierarchical_model/__log_sigma_beta',
'values_6': 'hierarchical_model/__log_eps'}
Graph Normalization
In general, we don’t want our “patterns” to be “brittle”, e.g. rely on explicit–yet variable–term orderings in commutative operators (e.g. a pattern that exclusively targets mt.add(x_lv, y_lv) and won’t match the equivalent mt.add(y_lv, x_lv)).
The grappler library in TensorFlow provides a subset of graph pruning/optimization steps. Ideally, a library like grappler would provide full-fledged graph normalization/canonicalization upon which we could base the subgraphs used in our relations.
While grappler does appear to provide some minimal algebraic normalizations, the extent to which these are performed and their breadth of relevant operator coverage isn’t clear; however, the normalizations that it does provide are worth using, so we’ll make use of them throughout.
Listing 17 provides a simple means of applying grappler.
from tensorflow.core.protobuf import config_pb2
from tensorflow.python.framework import ops
from tensorflow.python.framework import importer
from tensorflow.python.framework import meta_graph
from tensorflow.python.grappler import cluster
from tensorflow.python.grappler import tf_optimizer
try:
gcluster = cluster.Cluster()
except tf.errors.UnavailableError:
pass
config = config_pb2.ConfigProto()
def normalize_tf_graph(graph_output, graph_inputs=[]):
"""Use grappler to normalize a graph.
Arguments
=========
graph_output: Tensor
A tensor we want to consider as "output" of a FuncGraph.
graph_inputs: list of Tensor (optional)
Any tensors that correspond to inputs for the given output node.
Returns
=======
The simplified graph.
"""
train_op = graph_output.graph.get_collection_ref(ops.GraphKeys.TRAIN_OP)
train_op.clear()
train_op.extend([graph_output] + graph_inputs)
# if graph_inputs is not None:
# # ops.GraphKeys.MODEL_VARIABLES?
# train_vars = graph_output.graph.get_collection_ref(ops.GraphKeys.TRAINABLE_VARIABLES),
# train_vars.clear()
# train_vars.extend(graph_inputs)
metagraph = meta_graph.create_meta_graph_def(graph=graph_output.graph)
optimized_graphdef = tf_optimizer.OptimizeGraph(
config, metagraph, verbose=True, cluster=gcluster)
optimized_graph = ops.Graph()
with optimized_graph.as_default():
importer.import_graph_def(optimized_graphdef, name="")
opt_graph_output = optimized_graph.get_tensor_by_name(graph_output.name)
return opt_graph_outputIn Listing 17 we run grappler on the log-likelihood graph for a normal random variable from Listing 10.
normal_log_lik_opt = normalize_tf_graph(normal_log_lik)Listing 19 compares the computed outputs for the original and normalized graphs–given identical inputs.
res_unopt = normal_log_lik.eval({'mu:0': np.r_[3], 'tau:0': np.r_[1], 'value:0': np.r_[1]},
session=tf.compat.v1.Session(graph=normal_log_lik.graph))
res_opt = normal_log_lik_opt.eval({'mu:0': np.r_[3], 'tau:0': np.r_[1], 'value:0': np.r_[1]},
session=tf.compat.v1.Session(graph=normal_log_lik_opt.graph))
# They should be equal, naturally
assert np.array_equal(res_unopt, res_opt)
_ = [res_unopt, res_opt][array([-2.9189386], dtype=float32), array([-2.9189386], dtype=float32)]tf_dprint(normal_log_lik_opt)Tensor(Sub):0, shape=[None] "Normal_1/log_prob/sub:0"
| Tensor(Mul):0, shape=[None] "Normal_1/log_prob/mul:0"
| | Tensor(SquaredDifference):0, shape=[None] "Normal_1/log_prob/SquaredDifference:0"
| | | Tensor(RealDiv):0, shape=[None] "Normal_1/log_prob/truediv:0"
| | | | Tensor(Placeholder):0, shape=[None] "value:0"
| | | | Tensor(Placeholder):0, shape=[None] "tau:0"
| | | Tensor(RealDiv):0, shape=[None] "Normal_1/log_prob/truediv_1:0"
| | | | Tensor(Placeholder):0, shape=[None] "mu:0"
| | | | Tensor(Placeholder):0, shape=[None] "tau:0"
| | Tensor(Const):0, shape=[] "Normal_1/log_prob/mul/x:0"
| | | -0.5
| Tensor(AddV2):0, shape=[None] "Normal_1/log_prob/add:0"
| | Tensor(Log):0, shape=[None] "Normal_1/log_prob/Log:0"
| | | Tensor(Placeholder):0, shape=[None] "tau:0"
| | Tensor(Const):0, shape=[] "Normal_1/log_prob/add/x:0"
| | | 0.9189385
From the output of Listing 21, we can see that grappler has performed some constant folding and has reordered the inputs in "add_1_1"–among other things.
miniKanren Transform Relations
In Listing 23, we create miniKanren functions that identify the aforementioned SquaredDifference “chains” and perform the re-centering/scaling substitutions.
from itertools import chain
from functools import partial
from unification import var, reify, unify
from kanren import run, eq, lall, conde
from kanren.goals import not_equalo
from kanren.core import goaleval
from symbolic_pymc.tensorflow.meta import mt
from symbolic_pymc.relations import buildo
from symbolic_pymc.relations.graph import graph_applyo, reduceo
from symbolic_pymc.etuple import ExpressionTuple, etuple
def onceo(goal):
"""A non-relational operator that yields only the first result from a relation."""
def onceo_goal(s):
nonlocal goal
g = reify(goal, s)
g_stream = goaleval(g)(s)
s = next(g_stream)
yield s
return onceo_goal
def tf_graph_applyo(relation, a, b):
"""Construct a `graph_applyo` goal that evaluates a relation only at tensor nodes in a meta graph.
Parameters
----------
relation: function
A binary relation/goal constructor function
a: lvar, meta graph, or etuple
The left-hand side of the relation.
b: lvar, meta graph, or etuple
The right-hand side of the relation
"""
def _expand_some_nodes(node):
if isinstance(node, mt.Tensor) and node.op is not None:
return etuple(node.operator, *node.inputs, eval_obj=node)
return None
gapplyo = partial(graph_applyo, relation, preprocess_graph=_expand_some_nodes)
return gapplyo(a, b)
def tfp_normal_log_prob(loc, scale):
log_unnormalized = -0.5 * tf.math.squared_difference(
x / scale, loc / scale)
log_normalization = 0.5 * np.log(2. * np.pi) + tf.math.log(scale)
return log_unnormalized - log_normalizationdef shift_squared_subso(in_graph, out_subs):
"""Construct a goal that produces transforms for chains like (y + x)**2, (x + z)**2."""
Y_lv, X_lv, mu_X_lv = var(), var(), var()
scale_Y_lv = var()
X_form_lv = mt.Placeholder(dtype=var(), shape=var(), name=var())
# The actual base object's placeholder might have `_user_specified_name` as
# an extra `op.node_def.attr`, so let's just make the entire NodeDef a
# logic variable.
X_form_lv.op.node_def = var()
mu_Y_lv = mt.realdiv(X_lv, scale_Y_lv, name=var())
# Y_T_reshaped_lv = mt.Transpose(mt.reshape(Y_lv, var(), name=var()), var())
Y_reshaped_lv = mt.reshape(Y_lv, var(), name=var())
sqr_diff_Y_lv = mt.SquaredDifference(
mt.realdiv(Y_reshaped_lv,
scale_Y_lv,
name=var()),
mu_Y_lv,
name=var())
def Y_sqrdiffo(in_g, out_g):
return lall(eq(in_g, sqr_diff_Y_lv),
# This just makes sure that we're only considering X's
# that are Placeholders.
eq(X_lv, X_form_lv))
scale_X_lv = var()
sqr_diff_X_lv = mt.SquaredDifference(
# Mul is only used because RealDiv with 1 is changed by grappler
# mt.realdiv(X_lv, X_denom_lv, name=var()),
mt.mul(scale_X_lv, X_lv, name=var()),
mu_X_lv,
name=var())
def X_sqrdiffo(in_g, out_g):
return eq(in_g, sqr_diff_X_lv)
Y_new_mt = mt.addv2(X_lv, mt.mul(scale_Y_lv, Y_lv))
Y_log_scale = mt.log(scale_Y_lv, name=var())
res = lall(
# The first (y - x/a)**2 (anywhere in the graph)
tf_graph_applyo(Y_sqrdiffo, in_graph, in_graph),
# The corresponding (x/b - z)**2 (also anywhere else in the graph)
tf_graph_applyo(X_sqrdiffo, in_graph, in_graph),
# Find the log-scale factor (at this point, we might as well match an
# entire normal log-likelihood!)
tf_graph_applyo(lambda x, y: eq(x, Y_log_scale), in_graph, in_graph),
# Not sure if we need this, but we definitely don't want X == Y
(not_equalo, [Y_lv, X_lv], True),
# Create replacement rule pairs
eq(out_subs, [[Y_lv, Y_new_mt],
[Y_log_scale, 0.0]]))
return resdef shift_squared_terms(in_obj, graph_inputs=[]):
"""Re-center/scale SquaredDifference terms corresponding to hierarchical normals."""
# Normalize and convert to a meta graph
in_obj = mt(normalize_tf_graph(in_obj, graph_inputs=graph_inputs))
# This run returns all the substitutions found in the graph
subs_lv = var()
subs_res = run(0, subs_lv, shift_squared_subso(in_obj, subs_lv))
if not subs_res:
print("Failed to find the required forms within the graph.")
return
# NOTE: We're only going to apply the first transformation pair for now.
subs_res = [subs_res[0]]
def subs_replaceo(in_g, out_g):
"""Create a goal that applies substitutions to a graph."""
def _subs_replaceo(in_g, out_g):
nonlocal subs_res
# Each result is a pair of replacement pairs:
# the first pair is the re-center/scale transform,
# the second pair is the cancellation of the log differential scale term.
subs_goals = [[eq(in_g, x), eq(out_g, y)]
for x, y in chain.from_iterable(subs_res)]
x_g = conde(*subs_goals)
return x_g
g = onceo(tf_graph_applyo(_subs_replaceo, in_g, out_g))
return g
# Apply each substitution once
out_graph_lv = var()
res = run(1, out_graph_lv, reduceo(subs_replaceo, in_obj, out_graph_lv))
if res:
def reify_res(graph_res):
"""Reconstruct and/or reify meta object results."""
from_etuple = graph_res.eval_obj if isinstance(graph_res, ExpressionTuple) else graph_res
if hasattr(from_etuple, 'reify'):
return from_etuple.reify()
else:
return from_etuple
res = [reify_res(r) for r in res]
if len(res) == 1 and isinstance(res[0], tf.Tensor):
graph_res = res[0]
return normalize_tf_graph(graph_res, graph_inputs=graph_inputs), subs_resAs a test, we will run our miniKanren relations on the log-likelihood graph for a normal-normal hierarchical model in Listing 26.
with graph_mode(), tf.Graph().as_default() as demo_graph:
X_tfp = tfp.distributions.normal.Normal(0.0, 1.0, name='X')
x_tf = tf.compat.v1.placeholder(tf.float32, name='value_x',
shape=tf.TensorShape([None]))
tau_tf = tf.compat.v1.placeholder(tf.float32, name='tau',
shape=tf.TensorShape([None]))
Y_tfp = tfp.distributions.normal.Normal(x_tf, tau_tf, name='Y')
y_tf = tf.compat.v1.placeholder(tf.float32, name='value_y',
shape=tf.TensorShape([None]))
y_T_reshaped = tf.transpose(tf.reshape(y_tf, []))
hier_norm_lik = tf.math.log(y_tf) + Y_tfp.log_prob(y_T_reshaped) + X_tfp.log_prob(x_tf)
hier_norm_lik = normalize_tf_graph(hier_norm_lik)Listing 27 shows the form that a graph representing a hierarchical normal-normal model will generally take in TFP.
tf_dprint(hier_norm_lik)Tensor(AddV2):0, shape=[None] "add_1:0"
| Tensor(Sub):0, shape=[None] "X_1/log_prob/sub:0"
| | Tensor(Mul):0, shape=[None] "X_1/log_prob/mul:0"
| | | Tensor(SquaredDifference):0, shape=[None] "X_1/log_prob/SquaredDifference:0"
| | | | Tensor(Mul):0, shape=[None] "X_1/log_prob/truediv:0"
| | | | | Tensor(Const):0, shape=[] "ConstantFolding/X_1/log_prob/truediv_recip:0"
| | | | | | 1.
| | | | | Tensor(Placeholder):0, shape=[None] "value_x:0"
| | | | Tensor(Const):0, shape=[] "X_1/log_prob/truediv_1:0"
| | | | | 0.
| | | Tensor(Const):0, shape=[] "Y_1/log_prob/mul/x:0"
| | | | -0.5
| | Tensor(Const):0, shape=[] "Y_1/log_prob/add/x:0"
| | | 0.9189385
| Tensor(AddV2):0, shape=[None] "add:0"
| | Tensor(Log):0, shape=[None] "Log:0"
| | | Tensor(Placeholder):0, shape=[None] "value_y:0"
| | Tensor(Sub):0, shape=[None] "Y_1/log_prob/sub:0"
| | | Tensor(Mul):0, shape=[None] "Y_1/log_prob/mul:0"
| | | | Tensor(SquaredDifference):0, shape=[None] "Y_1/log_prob/SquaredDifference:0"
| | | | | Tensor(RealDiv):0, shape=[None] "Y_1/log_prob/truediv:0"
| | | | | | Tensor(Reshape):0, shape=[] "Reshape:0"
| | | | | | | Tensor(Placeholder):0, shape=[None] "value_y:0"
| | | | | | | Tensor(Const):0, shape=[0] "Reshape/shape:0"
| | | | | | | | []
| | | | | | Tensor(Placeholder):0, shape=[None] "tau:0"
| | | | | Tensor(RealDiv):0, shape=[None] "Y_1/log_prob/truediv_1:0"
| | | | | | Tensor(Placeholder):0, shape=[None] "value_x:0"
| | | | | | Tensor(Placeholder):0, shape=[None] "tau:0"
| | | | Tensor(Const):0, shape=[] "Y_1/log_prob/mul/x:0"
| | | | | -0.5
| | | Tensor(AddV2):0, shape=[None] "Y_1/log_prob/add:0"
| | | | Tensor(Log):0, shape=[None] "Y_1/log_prob/Log:0"
| | | | | Tensor(Placeholder):0, shape=[None] "tau:0"
| | | | Tensor(Const):0, shape=[] "Y_1/log_prob/add/x:0"
| | | | | 0.9189385
Listing 29 runs our transformation and Listing 32 prints the resulting graph.
with graph_mode(), demo_graph.as_default():
test_output_res, test_remaps = shift_squared_terms(hier_norm_lik, graph_inputs=[x_tf, y_tf])for rm in test_remaps:
for r in rm:
tf_dprint(r[0])
print("->")
tf_dprint(r[1])
print("------")Tensor(Placeholder):0, shape=[None] "value_y:0"
->
Tensor(AddV2):0, shape=[None] "AddV2:0"
| Tensor(Placeholder):0, shape=[None] "value_x:0"
| Tensor(Mul):0, shape=[None] "Mul:0"
| | Tensor(Placeholder):0, shape=[None] "tau:0"
| | Tensor(Placeholder):0, shape=[None] "value_y:0"
------
Tensor(Log):0, shape=~_12312 "Y_1/log_prob/Log:0"
| Tensor(Placeholder):0, shape=[None] "tau:0"
->
0.0
------
tf_dprint(test_output_res)Tensor(AddV2):0, shape=[None] "add_1_1:0"
| Tensor(Sub):0, shape=[None] "X_1/log_prob/sub:0"
| | Tensor(Mul):0, shape=[None] "X_1/log_prob/mul:0"
| | | Tensor(SquaredDifference):0, shape=[None] "X_1/log_prob/SquaredDifference:0"
| | | | Tensor(Mul):0, shape=[None] "X_1/log_prob/truediv:0"
| | | | | Tensor(Const):0, shape=[] "ConstantFolding/X_1/log_prob/truediv_recip:0"
| | | | | | 1.
| | | | | Tensor(Placeholder):0, shape=[None] "value_x:0"
| | | | Tensor(Const):0, shape=[] "X_1/log_prob/truediv_1:0"
| | | | | 0.
| | | Tensor(Const):0, shape=[] "Y_1/log_prob/mul/x:0"
| | | | -0.5
| | Tensor(Const):0, shape=[] "Y_1/log_prob/add/x:0"
| | | 0.9189385
| Tensor(AddV2):0, shape=[None] "add_2:0"
| | Tensor(Log):0, shape=[None] "Log_1:0"
| | | Tensor(AddV2):0, shape=[None] "AddV2:0"
| | | | Tensor(Mul):0, shape=[None] "Mul:0"
| | | | | Tensor(Placeholder):0, shape=[None] "tau:0"
| | | | | Tensor(Placeholder):0, shape=[None] "value_y:0"
| | | | Tensor(Placeholder):0, shape=[None] "value_x:0"
| | Tensor(Sub):0, shape=[None] "Y_1/log_prob/sub_1:0"
| | | Tensor(Mul):0, shape=[None] "Y_1/log_prob/mul_1:0"
| | | | Tensor(SquaredDifference):0, shape=[None] "Y_1/log_prob/SquaredDifference_1:0"
| | | | | Tensor(RealDiv):0, shape=[None] "Y_1/log_prob/truediv_1:0"
| | | | | | Tensor(Placeholder):0, shape=[None] "value_x:0"
| | | | | | Tensor(Placeholder):0, shape=[None] "tau:0"
| | | | | Tensor(RealDiv):0, shape=[None] "Y_1/log_prob/truediv_2:0"
| | | | | | Tensor(Reshape):0, shape=[] "Reshape_1:0"
| | | | | | | Tensor(AddV2):0, shape=[None] "AddV2:0"
| | | | | | | | ...
| | | | | | | Tensor(Const):0, shape=[0] "Reshape/shape:0"
| | | | | | | | []
| | | | | | Tensor(Placeholder):0, shape=[None] "tau:0"
| | | | Tensor(Const):0, shape=[] "Y_1/log_prob/mul/x:0"
| | | | | -0.5
| | | Tensor(Const):0, shape=[] "Y_1/log_prob/add/x:0"
| | | | 0.9189385
Missing Graph Simplifications
From Listing 32 we can see that grappler is not applying enough algebraic simplifications (e.g. it doesn’t remove multiplications with 1 or reduce the \(\left(\mu + x - \mu \right)^2\) term in SquaredDifference).
Does missing this simplification amount to anything practical? Listing 34 demonstrates the difference between our model without the simplification and a manually constructed model without the redundancy in SquaredDifference.
def compute_point_diff():
with graph_mode(), demo_graph.as_default():
Y_trans_tfp = tfp.distributions.normal.Normal(0.0, 1.0, name='Y_trans')
y_shifted_tf = x_tf + tau_tf * y_tf
hier_norm_trans_lik = tf.math.log(y_shifted_tf) + Y_trans_tfp.log_prob(y_T_reshaped) + X_tfp.log_prob(x_tf)
hier_norm_trans_lik = normalize_tf_graph(hier_norm_trans_lik)
test_point = {x_tf.name: np.r_[1.0],
tau_tf.name: np.r_[1e-20],
y_tf.name: np.r_[1000.1]}
with tf.compat.v1.Session(graph=test_output_res.graph).as_default():
val = test_output_res.eval(test_point)
with tf.compat.v1.Session(graph=hier_norm_trans_lik.graph).as_default():
val_2 = hier_norm_trans_lik.eval(test_point)
return val, val_2_ = np.subtract(*compute_point_diff())[500099.94]The output of Listing 35 shows exactly how large the discrepancy can be for carefully chosen parameter values. More specifically, as tau_tf gets smaller and the magnitude of the difference x_tf - y_tf gets larger, the discrepancy can increase. Since such parameter values are likely to be visited during sampling, we should address this missing simplification.
In Listing 38 we create a goal that performs that aforementioned simplification for SquaredDifference.
def recenter_sqrdiffo(in_g, out_g):
"""Create a goal that essentially reduces `(a / d - (a + d * c) / d)**2` to `d**2`"""
a_sqd_lv, b_sqd_lv, d_sqd_lv = var(), var(), var()
# Pattern: (a / d - b / d)**2
target_sqrdiff_lv = mt.SquaredDifference(
mt.realdiv(a_sqd_lv, d_sqd_lv, name=var()),
mt.realdiv(b_sqd_lv, d_sqd_lv, name=var()),
name=var()
)
# Pattern: d * c + a
c_sqd_lv = var()
b_part_lv = mt.addv2(mt.mul(d_sqd_lv, c_sqd_lv, name=var()), a_sqd_lv, name=var())
# Replacement: c**2
simplified_sqrdiff_lv = mt.SquaredDifference(
c_sqd_lv,
0.0
)
reshape_lv = var()
simplified_sqrdiff_reshaped_lv = mt.SquaredDifference(
mt.reshape(c_sqd_lv, reshape_lv),
0.0
)
res = lall(
# input == (a / d - b / d)**2 must be "true"
eq(in_g, target_sqrdiff_lv),
# "and"
conde([
# "if" b == d * c + a is "true"
eq(b_sqd_lv, b_part_lv),
# "then" output == (c - 0)**2 is also "true"
eq(out_g, simplified_sqrdiff_lv)
# "or"
], [
# We have to use this to cover some variation also not
# sufficiently/consistently "normalized" by `grappler`.
# "if" b == reshape(d * c + a, ?) is "true"
eq(b_sqd_lv, mt.reshape(b_part_lv, reshape_lv, name=var())),
# "then" output == (reshape(c, ?) - 0)**2 is also "true"
eq(out_g, simplified_sqrdiff_reshaped_lv)
]))
return resWe apply the simplification in Listing 38 and print the results in 39.
with graph_mode(), test_output_res.graph.as_default():
res = run(1, var('q'),
reduceo(lambda x, y: tf_graph_applyo(recenter_sqrdiffo, x, y),
test_output_res, var('q')))
test_output_res = normalize_tf_graph(res[0].eval_obj.reify())tf_dprint(test_output_res.graph.get_tensor_by_name('SquaredDifference:0'))Tensor(SquaredDifference):0, shape=[None] "SquaredDifference:0"
| Tensor(Const):0, shape=[] "X_1/log_prob/truediv_1:0"
| | 0.
| Tensor(Placeholder):0, shape=[None] "value_y:0"
After simplification, the difference is now gone.
_ = np.subtract(*compute_point_diff())[0.]Transforming the Log-likelihood Graph
Now, we’re ready to apply the transform to the radon model log-likelihood graph.
with graph_mode(), tf.Graph().as_default() as trans_graph:
graph_inputs = [logpfn_fg.get_operation_by_name(i.name).outputs[0]
for i in logpfn_cf.structured_input_signature[0]]
logpfn_trans_tf, logpfn_remaps = shift_squared_terms(logpfn_fg.outputs[0], graph_inputs=graph_inputs)
with graph_mode(), logpfn_trans_tf.graph.as_default():
res = run(1, var('q'),
reduceo(lambda x, y: tf_graph_applyo(recenter_sqrdiffo, x, y),
logpfn_trans_tf, var('q')))
logpfn_trans_tf = normalize_tf_graph(res[0].eval_obj.reify())Listing 44 shows the replacements that were made throughout the graph. Two replacements were found and they appear to correspond to the un-centered normal distribution terms a and b in our model–as intended.
for rm in logpfn_remaps:
for r in rm:
tf_dprint(r[0])
print("->")
tf_dprint(r[1])
print("------")Tensor(Placeholder):0, shape=[85] "values_2:0"
->
Tensor(AddV2):0, shape=[85] "AddV2:0"
| Tensor(Placeholder):0, shape=[] "values_4:0"
| Tensor(Mul):0, shape=[85] "Mul_4:0"
| | Tensor(Exp):0, shape=[] "exp_2_1/forward/Exp:0"
| | | Tensor(Placeholder):0, shape=[] "values_5:0"
| | Tensor(Placeholder):0, shape=[85] "values_2:0"
------
Tensor(Log):0, shape=~_175065 "SampleNormal_3_1/log_prob/Normal_3/log_prob/Log:0"
| Tensor(Exp):0, shape=[] "exp_2_1/forward/Exp:0"
| | Tensor(Placeholder):0, shape=[] "values_5:0"
->
0.0
------
Likewise, Listing 46 shows SquaredDifference subgraphs that appear in the transformed log-likelihood.
square_diff_outs = [o.outputs[0] for o in logpfn_trans_tf.graph.get_operations()
if o.type == 'SquaredDifference' or
o.type.startswith('Gather') or o.type == 'Log']
for t in square_diff_outs:
tf_dprint(t)Tensor(GatherV2):0, shape=[919] "GatherV2:0"
| Tensor(Placeholder):0, shape=[85] "values_3:0"
| Tensor(Const):0, shape=[919] "GatherV2/indices:0"
| | [ 0 0 0 ... 83 84 84]
| Tensor(Const):0, shape=[] "GatherV2/axis:0"
| | 0
Tensor(Log):0, shape=[] "SampleNormal_2_1/log_prob/Normal_2/log_prob/Log:0"
| Tensor(Exp):0, shape=[] "exp_1/forward/Exp:0"
| | Tensor(Placeholder):0, shape=[] "values_0:0"
Tensor(SquaredDifference):0, shape=[] "Normal_5/log_prob/SquaredDifference:0"
| Tensor(Const):0, shape=[] "Const_723:0"
| | 0.
| Tensor(Mul):0, shape=[] "Normal_5/log_prob/truediv:0"
| | Tensor(Const):0, shape=[] "exp_3_2/inverse_log_det_jacobian/mul_1:0"
| | | 1.
| | Tensor(Placeholder):0, shape=[] "values_1:0"
Tensor(SquaredDifference):0, shape=[85] "SquaredDifference:0"
| Tensor(Const):0, shape=[] "Const_723:0"
| | 0.
| Tensor(Reshape):0, shape=[85] "Reshape:0"
| | Tensor(Placeholder):0, shape=[85] "values_2:0"
| | Tensor(Const):0, shape=[1] "SampleNormal_2_1/log_prob/Reshape/shape:0"
| | | [85]
Tensor(SquaredDifference):0, shape=[] "Normal_1_1/log_prob/SquaredDifference:0"
| Tensor(Const):0, shape=[] "Const_723:0"
| | 0.
| Tensor(Mul):0, shape=[] "Normal_1_1/log_prob/truediv:0"
| | Tensor(Const):0, shape=[] "exp_3_2/inverse_log_det_jacobian/mul_1:0"
| | | 1.
| | Tensor(Placeholder):0, shape=[] "values_4:0"
Tensor(Log):0, shape=[] "Normal_4_1/log_prob/Log:0"
| Tensor(Exp):0, shape=[] "exp_3_1/forward/Exp:0"
| | Tensor(Placeholder):0, shape=[] "values_6:0"
Tensor(SquaredDifference):0, shape=[85] "SampleNormal_2_1/log_prob/Normal_2/log_prob/SquaredDifference:0"
| Tensor(RealDiv):0, shape=[85] "SampleNormal_2_1/log_prob/Normal_2/log_prob/truediv:0"
| | Tensor(Reshape):0, shape=[85] "SampleNormal_2_1/log_prob/Reshape:0"
| | | Tensor(Placeholder):0, shape=[85] "values_3:0"
| | | Tensor(Const):0, shape=[1] "SampleNormal_2_1/log_prob/Reshape/shape:0"
| | | | [85]
| | Tensor(Exp):0, shape=[] "exp_1/forward/Exp:0"
| | | Tensor(Placeholder):0, shape=[] "values_0:0"
| Tensor(RealDiv):0, shape=[] "SampleNormal_2_1/log_prob/Normal_2/log_prob/truediv_1:0"
| | Tensor(Placeholder):0, shape=[] "values_1:0"
| | Tensor(Exp):0, shape=[] "exp_1/forward/Exp:0"
| | | ...
Tensor(GatherV2):0, shape=[919] "GatherV2_1_1:0"
| Tensor(AddV2):0, shape=[85] "AddV2:0"
| | Tensor(Mul):0, shape=[85] "Mul_4:0"
| | | Tensor(Exp):0, shape=[] "exp_2_1/forward/Exp:0"
| | | | Tensor(Placeholder):0, shape=[] "values_5:0"
| | | Tensor(Placeholder):0, shape=[85] "values_2:0"
| | Tensor(Placeholder):0, shape=[] "values_4:0"
| Tensor(Const):0, shape=[919] "GatherV2/indices:0"
| | [ 0 0 0 ... 83 84 84]
| Tensor(Const):0, shape=[] "GatherV2/axis:0"
| | 0
Tensor(SquaredDifference):0, shape=[919] "Normal_4_1/log_prob/SquaredDifference_1:0"
| Tensor(RealDiv):0, shape=[919] "Normal_4_1/log_prob/truediv:0"
| | Tensor(Const):0, shape=[919] "Normal_4_1/log_prob/value:0"
| | | [0.8329091 0.8329091 1.0986123 ... 1.6292405 1.3350011 1.0986123]
| | Tensor(Exp):0, shape=[] "exp_3_1/forward/Exp:0"
| | | Tensor(Placeholder):0, shape=[] "values_6:0"
| Tensor(RealDiv):0, shape=[919] "Normal_4_1/log_prob/truediv_1_1:0"
| | Tensor(AddV2):0, shape=[919] "add_12:0"
| | | Tensor(GatherV2):0, shape=[919] "GatherV2:0"
| | | | Tensor(Placeholder):0, shape=[85] "values_3:0"
| | | | Tensor(Const):0, shape=[919] "GatherV2/indices:0"
| | | | | [ 0 0 0 ... 83 84 84]
| | | | Tensor(Const):0, shape=[] "GatherV2/axis:0"
| | | | | 0
| | | Tensor(Mul):0, shape=[919] "mul_5:0"
| | | | Tensor(GatherV2):0, shape=[919] "GatherV2_1_1:0"
| | | | | Tensor(AddV2):0, shape=[85] "AddV2:0"
| | | | | | Tensor(Mul):0, shape=[85] "Mul_4:0"
| | | | | | | Tensor(Exp):0, shape=[] "exp_2_1/forward/Exp:0"
| | | | | | | | Tensor(Placeholder):0, shape=[] "values_5:0"
| | | | | | | Tensor(Placeholder):0, shape=[85] "values_2:0"
| | | | | | Tensor(Placeholder):0, shape=[] "values_4:0"
| | | | | Tensor(Const):0, shape=[919] "GatherV2/indices:0"
| | | | | | [ 0 0 0 ... 83 84 84]
| | | | | Tensor(Const):0, shape=[] "GatherV2/axis:0"
| | | | | | 0
| | | | Tensor(Const):0, shape=[919] "mul/y:0"
| | | | | [1. 0. 0. ... 0. 0. 0.]
| | Tensor(Exp):0, shape=[] "exp_3_1/forward/Exp:0"
| | | ...
Creating a new Log-likelihood Function
Now that we have a transformed version of the original log-likelihood graph (i.e. logpfn_trans_tf), we need to create a new FuncGraph from it. Listing 48 provides a simple function that creates a new ConcreteFunction from an updated output node.
from tensorflow.python.framework.func_graph import FuncGraph
from tensorflow.python.eager.function import ConcreteFunction
from tensorflow.python.eager.lift_to_graph import lift_to_graph
def new_tf_function(output, orig_cf):
"""Create a new ConcreteFunction by replacing a single output in an existing FuncGraph.
"""
orig_fg = orig_cf.graph
# with trans_graph.as_default(): #orig_fg.as_default():
logpfn_fg_new = FuncGraph('logpfn_new', orig_fg.collections, orig_fg.capture_by_value)
old_to_new_ops = lift_to_graph([output],
logpfn_fg_new,
add_sources=True,
handle_captures=True)
logpfn_fg_new.structured_input_signature = orig_fg.structured_input_signature
new_inputs = [old_to_new_ops.get(output.graph.get_operation_by_name(i.name).outputs[0])
for i in orig_cf.structured_input_signature[0]]
logpfn_fg_new.inputs = new_inputs
assert all(i is not None for i in logpfn_fg_new.inputs)
logpfn_fg_new.outputs = [old_to_new_ops[output]]
logpfn_fg_new.structured_outputs = logpfn_fg_new.outputs[0]
assert logpfn_fg_new.as_graph_element(logpfn_fg_new.outputs[0]) is not None
logpfn_new_cf = ConcreteFunction(logpfn_fg_new)
logpfn_new_cf._arg_keywords = orig_cf._arg_keywords
logpfn_new_cf._num_positional_args = len(logpfn_fg_new.inputs)
return logpfn_new_cflogpfn_new_cf = new_tf_function(logpfn_trans_tf, logpfn_cf)The new TF function, logpfn_new_cf, in Listing 48 is the function we are going to use for sampling from the new log-likelihood.
_ = logpfn_cf(*init.values()) - logpfn_new_cf(*init.values())tf.Tensor(153.41016, shape=(), dtype=float32)Listing 50 shows the difference between a transformed and non-transformed log-likelihood value given the same inputs.
Sampling from the new Log-likelihood
In Listing 53, we reproduce the remaining steps of pm.inference.sampling.sample and–unnaturally–force the PyMC4 machinery to draw samples from our new transformed log-likelihood function.
from contextlib import contextmanager
# We need to create new initial values for our transformed variables.
new_val_map = {}
for logpfn_remap in logpfn_remaps:
transed_var = logpfn_remap[0][0].reify()
transed_var_pymc_name = tfp_names_to_pymc[transed_var.op.name]
old_val_np = init[transed_var_pymc_name].numpy()
new_val_np = np.random.standard_normal(old_val_np.shape).astype(old_val_np.dtype)
new_val_map[transed_var_pymc_name] = tf.convert_to_tensor(new_val_np)
new_init = init.copy()
new_init.update(new_val_map)
@contextmanager
def pymc4_force_logp(logpfn_new_cf, new_init):
"""Temporarily fix the logp function and init values used by PyMC4's sampler."""
def _new_build_logp_function(*args, **kwargs):
nonlocal logpfn_new_cf, new_init
return logpfn_new_cf, new_init
_old_fn = pm.inference.sampling.build_logp_function
pm.inference.sampling.build_logp_function = _new_build_logp_function
try:
yield
finally:
pm.inference.sampling.build_logp_function = _old_fnwith pymc4_force_logp(logpfn_new_cf, new_init):
az_trace = sample(model)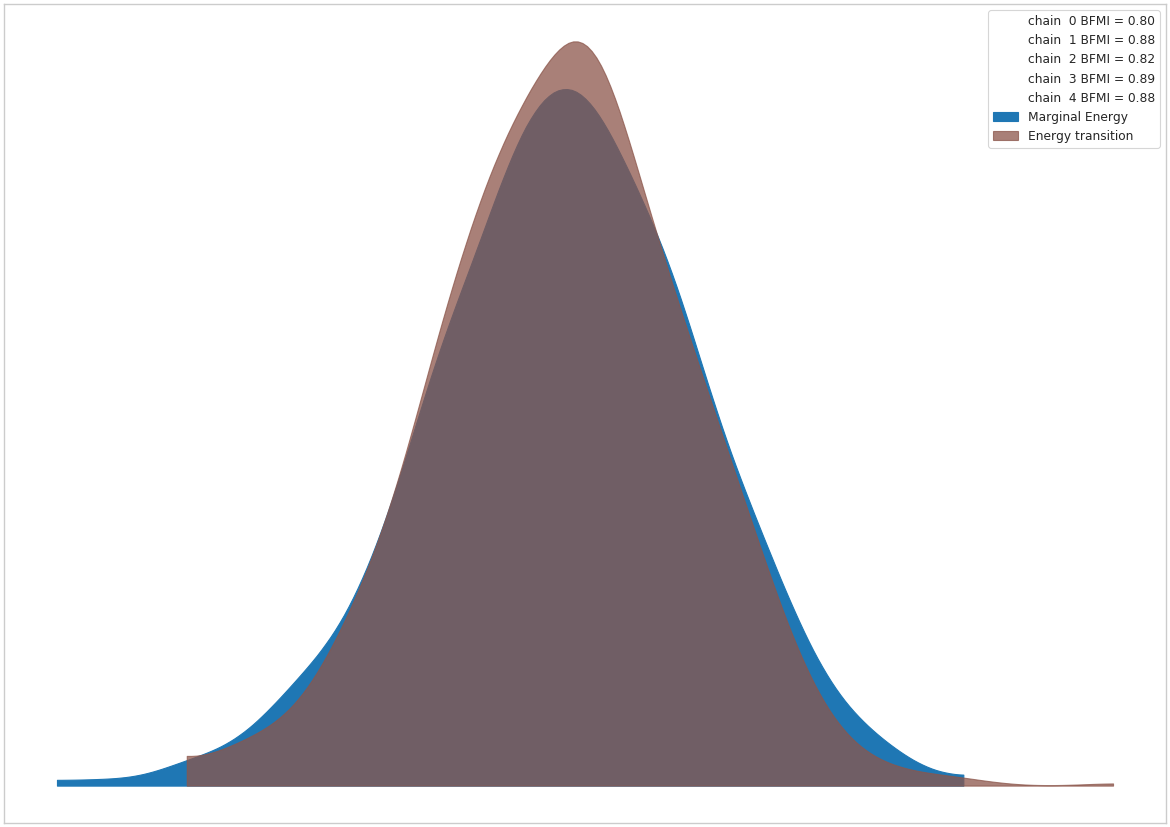
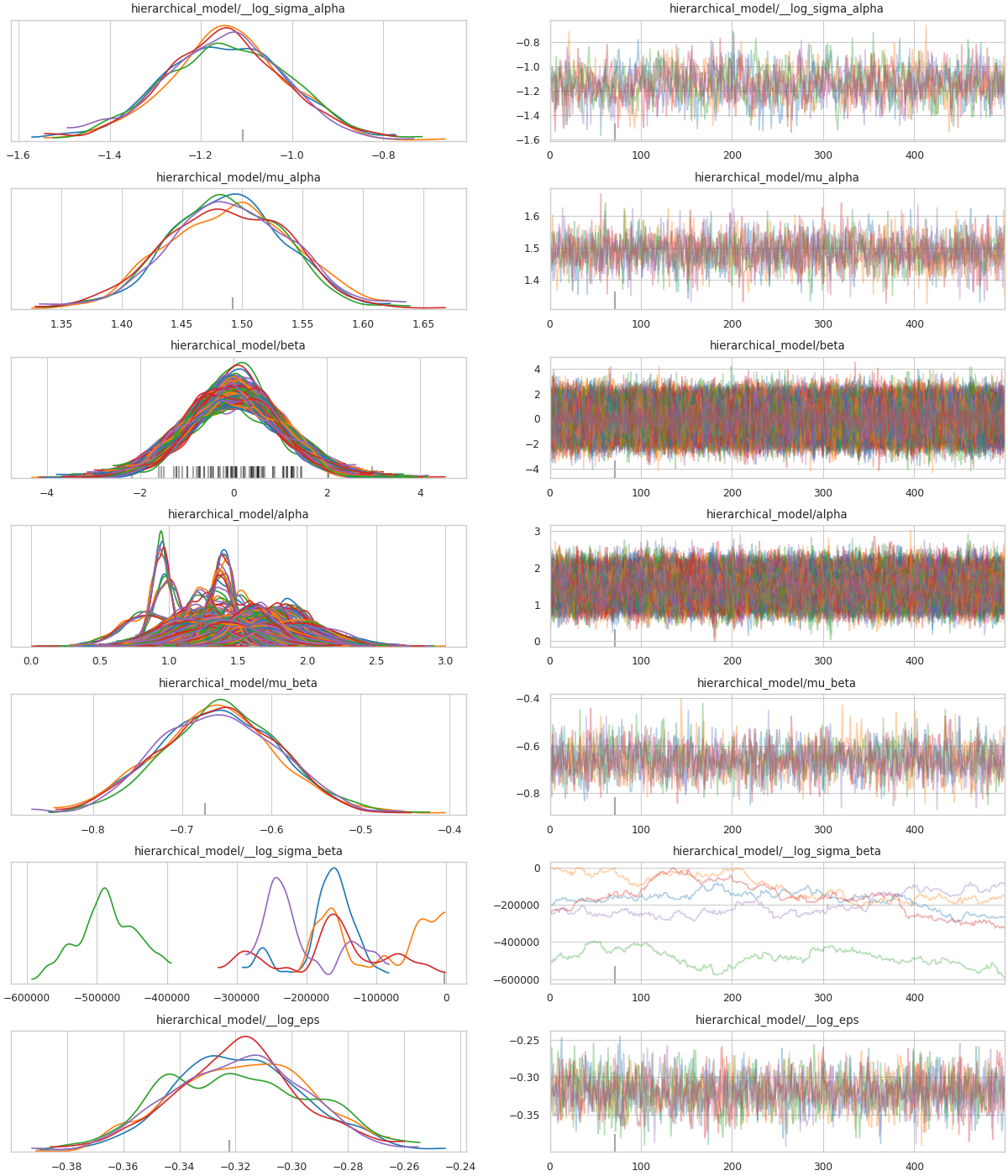
Discussion
The goals in the two separate run calls we used in Listing 23 could have been combined into a single run. This could’ve been accomplished using some “meta” steps (e.g. construct and evaluate a goal on-the-fly within a miniKanren) or special goals for reading from a miniKanren-generated dicts or association lists. Goals of this nature are not uncommon (e.g. type inference and inhabitation exmaples), and serve to demonstrate the great breadth of activity possible within relational context of miniKanren.
However, the point we want to make doesn’t require much sophistication. Instead, we wanted to demonstrate how a non-trivial “pattern” can be specified and matched using symbolic-pymc, and how easily those results could be used to transform a graph.
More specifically, our goal shift_squared_subso in 23 demonstrates the way in which we were able to specify desired structure(s) within a graph. We defined one pattern, Y_sqrdiffo, to match anywhere in the graph then another pattern, X_sqrdiffo, that relied on matched terms from Y_sqrdiffo and could also be matched/found anywhere else in the same graph.
Furthermore, our substitutions needed information from both “matched” subgraphs. Specifically, substitution pairs similar to (x, z + x). Within this framework, we could just as easily have included y–or any terms from either successfully matched subgraph–in the substitution expressions.
In sample-space, the search patterns and substitutions are much easier to specify exactly because they’re single-subgraph patterns that themselves are the subgraphs to be replaced (i.e. if we find a non-standard normal, replace it with a shifted/scaled standard normal). In log-space, we chose to find distinct subgraph “chains”, i.e. all (y - x)**2 and (x - z)**2 pairs (i.e. “connected” by an “unknown” term x), since these are produced by the log-likelihood form of hierarchical normal distributions.
As a result, we had a non-trivial structure/“pattern” to express–and execute. Using conventional graph search-and-replace functionality would’ve required much more orchestration and resulted considerably less flexible code with little-to-no reusability. In our case, the goals onceo and tf_graph_applyo are universal and the forms in shift_squared_subso can be easily changed to account for more sophisticated (or entirely distinct) patterns and substitutions.
Most related graph manipulation offerings make it easy to find a single subgraph that matches a pattern, but not potentially “co-dependent” and/or distinct subgraphs. In the end, the developer will often have to manually implement a “global” state and orchestrate multiple single-subgraph searches and their results.
For single search-and-replace objectives, this amount of manual developer intervention/orchestration might be excusable; however, for objectives requiring the evaluation of multiple graph transformation, this approach is mostly unmaintainable and extremely difficult to compartmentalize.
This demonstration barely even scratches the surface of what’s possible using miniKanren and relational programming for graph manipulation and symbolic statistical model optimization. As the symbolic-pymc project advances, we’ll cover examples in which miniKanren’s more distinct offerings are demonstrated.
Comments
comments powered by Disqus