- Introduction
- The Hidden Markov Model
- Sampling Model Graphs
- Log-likelihood
- PyMC3
Distributions - Discussion
Introduction
This document describes how Theano graphs can be used as a focal point for Bayesian model specification, and how these graphs can be bridged with PyMC3 objects and–as a result–produce a dramatically more robust and simplified foundation for PyMC3.
Yes, PyMC3 does use Theano–and, thus, Theano graphs–but it doesn’t explicitly build a graph for the relationships between random variables. In the following, we call such graphs [Theano] sample-space graphs and we’ll show how all the forms of sampling performed by PyMC3 (i.e. prior and posterior predictive) can be implemented using these graphs. We’ll also demonstrate how the log-likelihood graphs currently used by PyMC3 can be constructed from such graphs.
Before we go any further, let’s look at a simple example of a sample-space graph.
Consider the model in Equation .
\[\begin{equation} \label{eq:simple-model} Y = a Z + b, \quad Z \sim \operatorname{N}\left( 0, \sigma^2 \right) \;, \end{equation}\]
Equation can be represented by the Theano graph in Listing 1.
import theano
import theano.tensor as tt
from symbolic_pymc.theano.random_variables import NormalRV
a_tt = tt.vector('a')
b_tt = tt.vector('b')
sigma_tt = tt.scalar('sigma')
Z_rv = NormalRV(0, sigma_tt**2, name='Z')
Y_rv = a_tt * Z_rv + b_ttWhen \(Y\) is an observed variable, the Theano graph represented by Y_rv is our sample-space graph of interest. The graph for Z_rv is also a sample-space graph, and, in some cases, we’ll refer to Y_rv as a model graph due to its more direct correspondence to a model of interest (e.g. Equation ).
Naturally, the Theano tensors objects Z_rv and Y_rv are random variables, but–more specifically–the former is a direct output of a RandomVariable operator, while the latter is a function of the aforementioned RandomVariable output. This distinction will be important in what follows, but it suffices to say that both represent random draws from a distribution.
We can sample either of them–or both–by simply compiling the graphs into functions and evaluating those functions. This is demonstrated in Listing 2.
import numpy as np
Y_sampler = theano.function([a_tt, b_tt, sigma_tt], [Z_rv, Y_rv])
Y_sampler(np.r_[0.0, 1.0], np.r_[0.1, 0.3], 0.9)[array(-1.60047139), array([ 0.1 , -1.30047139])]Throughout this exposition we’ll use a non-trivial hidden Markov model (HMM) as our guiding example. These sorts of time-series are difficult to implement in PyMC3 due to their reliance on the challenging Scan function, symbolic shape issues in PyMC3, and the general complexity involved in writing their log-likelihoods and sampling functions–especially when one needs to iterate on hierarchical changes to such models. As a result, anything that can improve their ease of use within PyMC3 is a worthwhile consideration.
For other types of time-series that are represented and computed as Theano model graphs see Willard (2020). In those examples, custom samplers are constructed by hand in Theano; however, here we’re interested in using PyMC3 to generate posterior samples.
That said, we’ll demonstrate how the sample-space graphs for HMMs can be specified with relative ease, and we’ll build up to the construction of a custom PyMC3 Distribution class based entirely on transformations of the original sample-space graph.
Ultimately, the process of deriving this Distribution class demonstrates how all of the model information and objects required by PyMC3 can be derived from a sample-space graph. As a result, automation of this process would provide a new foundation for PyMC; one that can leverage Theano to perform all the complicated sampling and doesn’t suffer from the same symbolic shape limitations, and one for which it is much simpler to reason about a model systematically. This new PyMC would also set the stage for specialized optimizations that could dramatically improve performance.
Sampling Model Graphs
In this section, we show how all the sampling functionality of PyMC3 is already provided by Theano.
Prior Predictive Sampling
In Listing 7 we compile a Theano function that is able to draw samples from the model in Listing 6. More specifically, we created a function that computes \(\left( s_t, y_t \right) \sim \left( S_t, Y_t \right)\).
hmm_sampler = theano.function([], [S_rv, Y_rv])
theano_samples = hmm_sampler()
theano_samples = dict(zip(["S_rv", "Y_rv"], theano_samples))The samples produced by the compiled function hmm_sampler are effectively the same type of samples that pymc3.sample_prior_predictive would produce; however, in this case, Theano automatically handles variable dependencies in a way that pymc3.sample_prior_predictive currently cannot–plus, it has all the advantages of Theano compilation (e.g. algebraic optimizations, C-compiled functions).
y_samples_df = pd.DataFrame(np.stack([theano_samples["Y_rv"], theano_samples["S_rv"]], axis=1),
columns=("y", "s"),
index=X_df.index)
axes = plot_split_timeseries(y_samples_df,
figsize=(15, 10),
use_twin=True,
twin_plot_kwargs={
"alpha": 0.8,
"linestyle": "--",
"drawstyle": "steps-pre"
})
for ax, alt_ax in axes:
alt_ax.yaxis.set_major_locator(MaxNLocator(integer=True))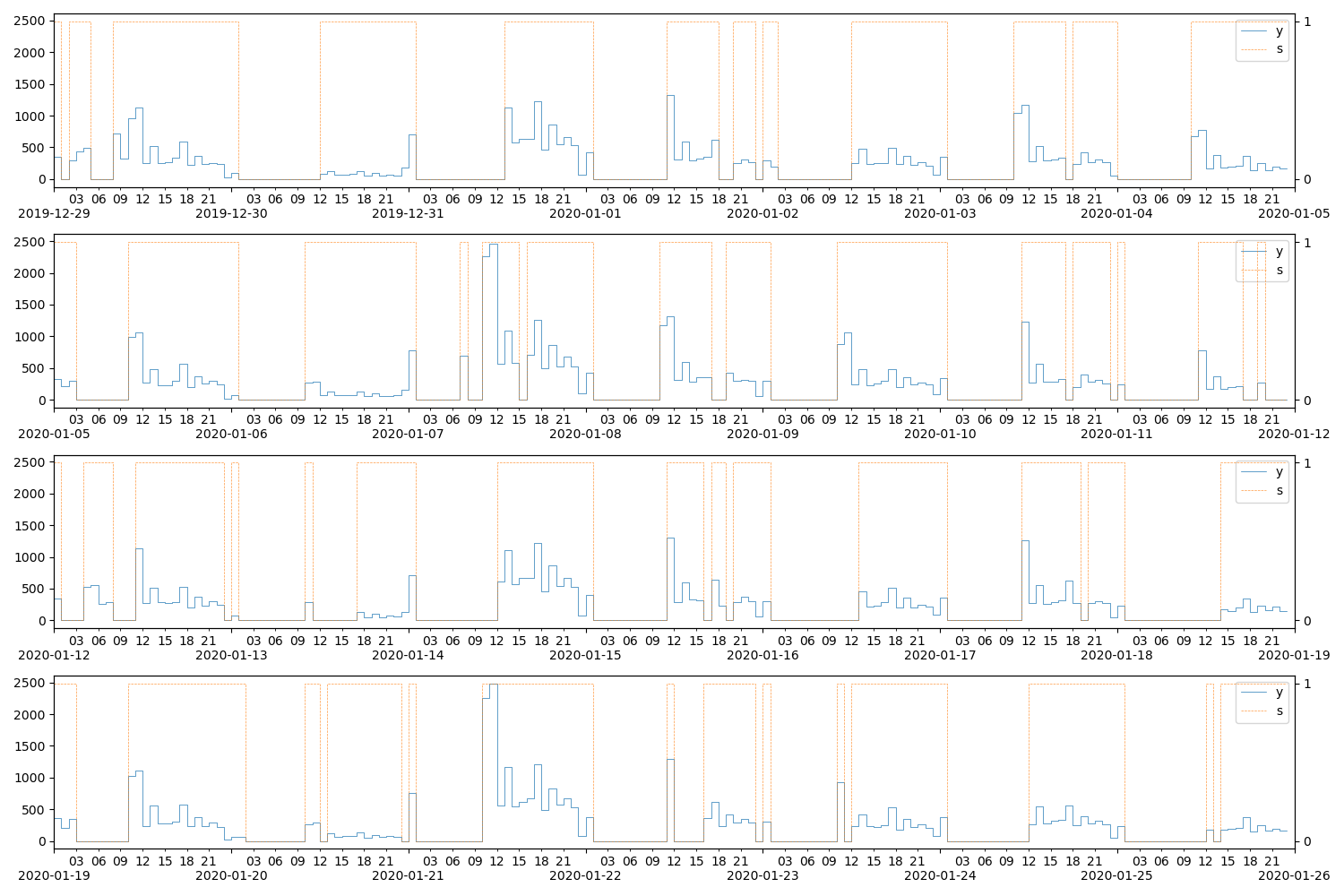
Figure 8 plots the samples in theano_samples. Unfortunately, sampling from the prior predictive produces very “random” series, but, if we wanted to–say–generate samples conditional on very specific values of the seasonal transition matrix parameters, \(\xi^{(S_t)}_t\), we could compile a different sampling function that takes those parameters as arguments. Simply put, we want a function that computes \(\left( s_t, y_t \right) \sim \left( S_t, Y_t \mid \xi^{(S_t)}_t \right)\).
Listing 9 compiles such a function in Theano and uses it draw samples given specific values of \(\xi^{(S_t)}_t\) that demonstrate higher probabilities of staying in–and transitioning to–the zero value state during weekdays and late hours.
import scipy as sp
xi_0_np = pd.Series(
# The coefficients used to compute the state zero-to-zero transition probabilities
# For two states, these are basically run through a logistic function, and
# the state zero-to-one transition probabilities are 1 minus the logistic
# values.
np.array([0.0] +
[0.0, 0.0, 0.0, 0.0, 0.0, -2.0, -2.0] +
[4.0] * 9 + list(-np.geomspace(1e-3, 3, num=13))),
index=X_df.columns)
xi_1_np = pd.Series(
# The coefficients for the state one-to-zero transition probabilities
np.array([-1.0] +
[0.5, 0.5, 0.5, 0.5, 0.5, -3.0, -3.0] +
[4.0] * 9 + list(-np.geomspace(1, 3, num=13))),
index=X_df.columns)
xis_np = np.stack([xi_0_np, xi_1_np], axis=1)[..., None]
hmm_cond_sampler = theano.function([xis_rv], [S_rv, Y_rv])
theano_samples = dict(zip(["S_rv", "Y_rv"], hmm_cond_sampler(xis_np)))y_samples_df = pd.DataFrame(np.stack([theano_samples["Y_rv"], theano_samples["S_rv"]], axis=1),
columns=("y", "s"),
index=X_df.index)
axes = plot_split_timeseries(y_samples_df,
figsize=(15, 10),
use_twin=True,
twin_plot_kwargs={
"alpha": 0.8,
"linestyle": "--",
"drawstyle": "steps-pre"
})
for ax, alt_ax in axes:
alt_ax.yaxis.set_major_locator(MaxNLocator(integer=True))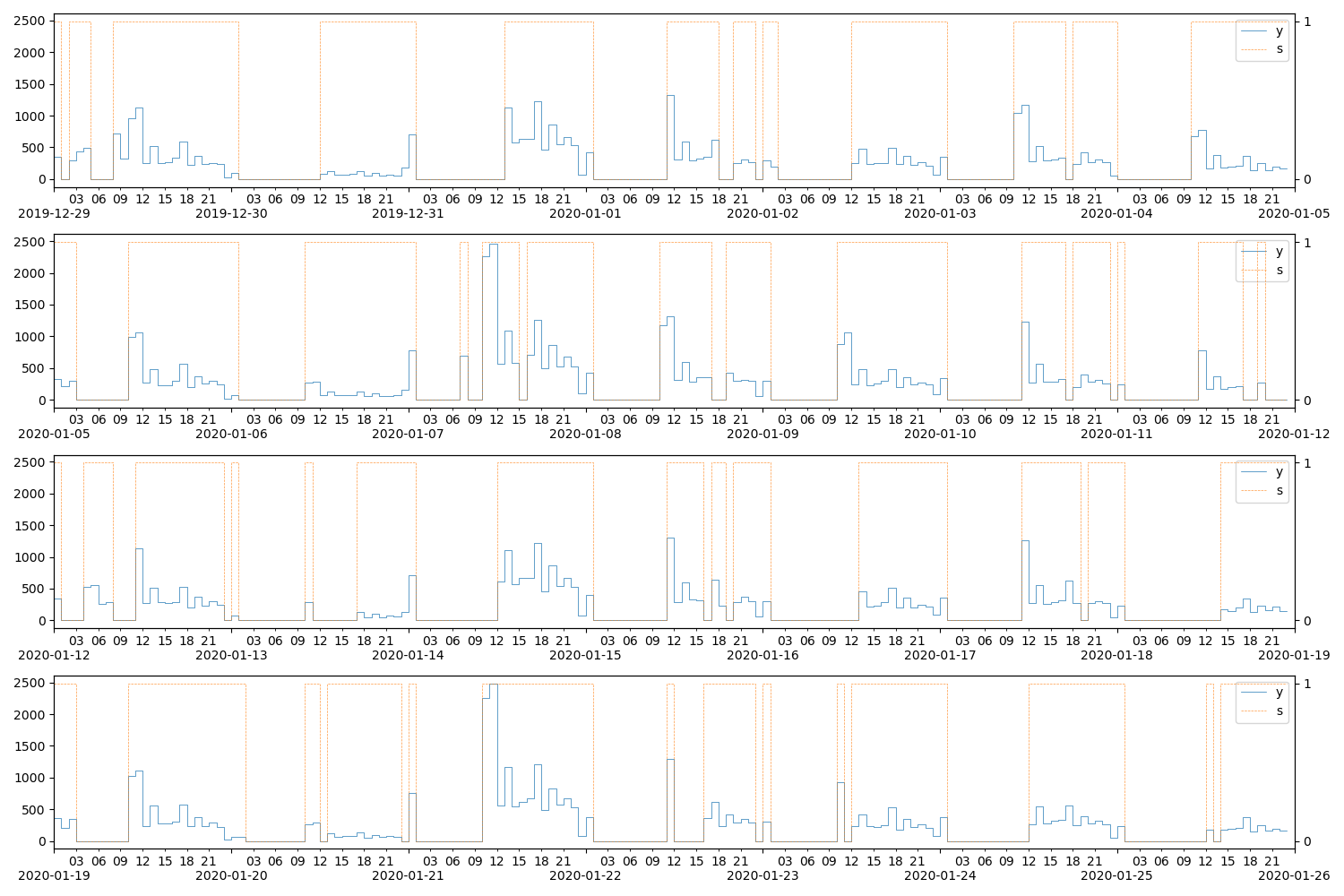
Posterior Predictive Sampling
Now that we know how to draw samples conditional on terms
posterior_samples = pm.sample(...)
#
# pm.sample_posterior_predictive(...)
#
posterior_samples = [{"S_rv": ..., }, {"S_rv": ...}, ..., {...}]
pp_samples = []
for sample_i in posterior_samples:
S_posteriors_i = sample_i['S_rv']
lambda_posteriors_i = sample_i['lambda_rv']
# xis_posteriors_i = [...]
pp_sample = Y_rv.distribution.random(point={
"S_rv": S_posteriors_i,
"lambda_rv": lambda_posteriors_i
})
pp_samples.append(pp_sample)Listing 12 demonstrates a fundamental limitation with the sample-space graph models: we can’t condition on arbitrary random variables.
from traceback import print_exc
S_rv_vals = S_rv.tag.test_value
lambda_vals = lambdas_tt.tag.test_value
try:
hmm_cond_sampler = theano.function([S_rv, lambdas_tt], Y_rv)
Y_rv_sim = hmm_cond_sampler(S_rv_vals, lambda_vals)
except Exception:
print_exc(limit=0)Traceback (most recent call last):
theano.compile.function_module.UnusedInputError: theano.function was asked to create a function computing outputs given certain inputs, but the provided input variable at index 0 is not part of the computational graph needed to compute the outputs: Subtensor{int64::}.0.
To make this error into a warning, you can pass the parameter on_unused_input='warn' to theano.function. To disable it completely, use on_unused_input='ignore'.
The problem is that our original sample-space model graph in Listing 6 generates the vector of all \(S_t\), \(S_{0:T}\), in the same Theano Scan that generate all the \(Y_t\); in other words, \(Y_{0:T}\) isn’t a function of \(S_{0:T}\) according the the Theano graph.
Simply put, we need to create a graph that “condition on” \(S_{0:T}\), or–in other words–convert the Scan output S_rv into an input.
def Y_given_S_step(S_t, emissions_t):
Y_t = emissions_t[S_t]
return Y_t
Y_given_S_rv, _ = theano.scan(fn=Y_given_S_step,
sequences=[S_rv, emissions_tt],
non_sequences=[],
outputs_info=[
{},
],
strict=True)
Y_sampler = theano.function([S_rv, lambdas_tt], Y_given_S_rv)
Y_given_S_np = Y_sampler(S_rv.tag.test_value, lambdas_tt.tag.test_value)Log-likelihood
In contrast to Theano sample-space graphs, there are Theano measure-space graphs, which–for our purposes–will correspond to Theano graphs that compute the log-likelihoods of terms in a model.
PyMC3 creates these kinds of Theano graphs in Distribution.logp–and the methods that call it.
Working from our original sample-space model graph in Listing 6, we can create a log-likelihood graph with a simple two-step process
- for each
RandomVariablecreate new variables to serve as inputs to a log-likelihood, then - replace each
RandomVariablewith its log-likelihood graphs–the latter being dependent on the previously created input variables.
Fortunately, we can use the existing Distribution.logp implementations to complete the second step.
To demonstrate, Listing 15 follows the above two steps in order to construct a log-likelihood graph for the \(S_0\) term.
# Create new variables for the values of `pi_0_rv` and `S_0_rv`
pi_0_in = tt.vector("pi_0")
S_0_in = tt.ivector("S_0")
# Create the log-likelihood graph for `S_0_rv`
S_0_ll = pm.Categorical.dist(pi_0_in).logp(S_0_in)The log-likelihood in Listing 15 is–of course–conditional on the \(\pi_0\) term, but we could easily create a joint log-likelihood by performing the same operation for \(\pi_0\) and adding the two log-likelihood graphs.
Unfortunately, more steps are needed when Scans are involved. If we want to create a log-likehood graph for \(S_{0:T}\), then–just like the conditional sample-space graph in Listing 14–we need to first transform the Scan so that it “conditions on” \(S_{0:T}\)–i.e. converts its output S_rv into an input.
S_in = tt.ivector("S")
def S_ll_step(S_t, S_tm1, Gamma_t):
S_ll_t = pm.Categorical.dist(Gamma_t[S_tm1]).logp(S_t)
return S_ll_t
S_ll, _ = theano.scan(fn=S_ll_step,
sequences=[
{"input": S_in, "taps": [0, -1]},
Gammas_tt,
],
outputs_info=[
{},
],
strict=True)The situation for \(Y_{0:T}\) is a little more complicated; it requires log-likelihood conversions in the emissions_tt term outside of the Scan and an update to the Scan so that it uses the log-likelihoods derived from emissions_tt. An implementation is given in Listing 17.
Y_in = tt.vector("Y")
lambdas_in = tt.vector("Y")
emissions_ll_tt = tt.stack([
pm.Constant.dist(0).logp(Y_in),
pm.Poisson.dist(lambdas_in).logp(Y_in)
], axis=1).squeeze()
def S_ll_step(S_t, emissions_ll_t, Gamma_t):
Y_ll_t = emissions_ll_t[S_t]
return Y_ll_t
Y_ll, _ = theano.scan(fn=S_ll_step,
sequences=[
S_in,
emissions_ll_tt,
Gammas_tt,
],
outputs_info=[
{},
],
strict=True)The functionality for automating these two steps in the non-Scan case already exist in symbolic-pymc, and the requisite functionality for simple case of Scan was introduced in #113 and #114.
The latter changes introduce a “push-out” optimization that helps expose RandomVariables hidden within the internal sub-graphs of Scan operators.
For instance, in the original Theano graph model, \(S_t\) is a RandomVariable created within the Scan operator’s inner-graph (via the step function run by Scan). Had \(S_t\) not been specified as an output of the inner function state_step, this “push-out” optimization would redefine the model so that it is.
Additionally, functions were added in #114 that automate the process of turning state_step into the Y_given_S_step in Listing 14. This is how we can automate the construction of conditional sample-space graphs and log-likelihood graphs.
PyMC3 Distributions
In order to use a complicated model like ours in Listing 6 within PyMC3, we need to construct a PyMC3 Distribution class using the conditional sampler functions and the log-likelihood graphs we derived above from the original model graph. Basically, the log-likelihood graphs comprise the body of the Distribution.logp method, and the conditional samplers comprise the Distribution.random method.
Unfortunately, the shape issues and sampler problems of PyMC3 aren’t actually removed in this process, since we’re moving out of the Theano framework in which those problems are solved.
Listing 18 constructs the Distribution class for \(Y_{0:T}\)–or Y_rv.
from pymc3.distributions.distribution import draw_values, _DrawValuesContext
class YRvDist(pymc3.Distribution):
def __init__(self, S, lambdas, **kwargs):
super().__init__(**kwargs)
self.S = S
self.lambdas = lambdas
def random(self, point=None, size=None):
with _DrawValuesContext() as draw_context:
# FIXME: Are we sure the "size" value in the tuple key will be `1`?
# This `_DrawValuesContext` confuses me.
term_smpl = draw_context.drawn_vars.get((self.states, 1), None)
if term_smpl is not None:
point[self.states.name] = term_smpl
S, lambdas = draw_values([self.S, self.lambdas], point=point, size=size)
res = Y_sampler(S, lambdas)
return res
def logp(self, y, s, lambdas):
log_lik = tt_clone(Y_ll, replacements={
Y_in: y,
S_in: s,
lambdas_in: lambdas,
})
return log_likThe Distribution objects constructed in this way can now be used to define and estimate a regular PyMC3 model, as demonstrated in Listing 19.
with pm.Model() as test_model:
S_rv = SRvDist("S")
lambdas_rv = LambdasRvDist("lambdas")
Y_rv = YRvDist("Y", S_rv, lambdas_rv, observed=y_tt)
with test_model:
posteriors = pm.sample()
with test_model:
pp_trace = pm.sample_posterior_predictive(posteriors, vars=['Y_rv'])Discussion
Regarding the compilation of Theano “model graphs” to PyMC3 (i.e. functionality that would allow us to produce posterior predictive samples using Theano while still being able to estimate), I’ve added most of the key functionality in PR #113 and #114.
Part of the functionality introduced there allows us to automatically produce new Theano graphs with inputs for each random variable dependency embedded in a Scan. It’s currently being used just to produce the log-likelihood graphs, but it’s also what we need in order to construct a fast Theano function that produces posterior predictive samples. Writing a posterior predictive sampler that does this is the next step.
The existing symbolic_pymc.theano.pymc3.graph_model function does this for simple Theano model graphs, but it does not work with the Scans we need to use in order to define time-series model graphs.
Bibliography
Willard, Dynamic Linear Models in Theano, Brandon T. Willard, (2020). link. ↩︎
Comments
comments powered by Disqus